Спектральный анализ ЭЭГ — метод математической обработки, направленный на количественную характеристику частотных диапазонов.
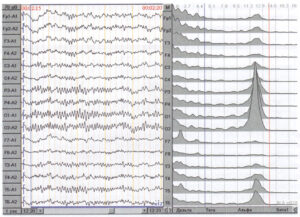
Любая волна на электроэнцефалограмме имеет два количественных параметра: период ее от пика до пика, выраженные во времени (величина, обратная периоду — частота волны, Гц) и амплитуда волны (в мкВ). Спектр ЭЭГ может быть отображен через амплитуду (мкВ), и тогда это — амплитудный спектр. Другим вариантом, более наглядным, является спектр мощности, где за мощность принято считать квадрат амплитуды волны, привязанный к временному отрезку, в котором выполнено измерение, — эпохе анализа (рис. 1). Значения мощности выражаются в виде показателей мкВ2 или мкВ2/Гц. Первый показатель отражает «суммарную мощность» какого-либо диапазона, второй — привязан к конкретным частотам.
В последнее время в связи с тем, что изучение доминирующих частот становится актуальным с позиции клинической трактовки, появилось понятие «мгновенное значение мощности», то есть это мощность на ЭЭГ, где установлен измеряющий ее курсор. Всякое «мгновение» имеет длительность, поэтому можно принять ее за 0,1 с, а размерность, следовательно, остается такой же, как у «суммарной мощности» — мкВ2.
Спектральный состав позволяет количественно оценить соотношение активности (ритмов) различных диапазонов частот. За выбранную эпоху анализа производится расчет общей мощности спектра по всему выбранному диапазону (например, от 0,5 до 35 Гц). Для каждого частотного диапазона (дельта, тета, альфа, бета) рассчитывается мощность диапазона, которая может быть выражена в абсолютных величинах мощности (мкВ2) или в относительных — как доля (в %) от общей мощности спектра.
Спектральный анализ в клинической электроэнцефалографии
Эквивалент спектрального анализа ЭЭГ каждый врач-нейрофизиолог всегда выполняет мысленно при визуально-логическом анализе, используя свой опыт, свою интуицию, оценивая где и сколько в наличии дельта-, тета-, альфа-и бета-волн. Поэтому спектральный анализ как дополнительное приложение к традиционному анализу ЭЭГ не воспринимается как нечто необычное. Даже описательная характеристика спектральных графиков по отведениям сходна с таковой нативной ЭЭГ. Используются практически те же термины и характеристики (локализация, выраженность, степень асимметрии, распространенность и т. д.). Однако графики спектрального анализа определенно снижают степень субъективности в оценке таких понятий, как дезорганизация, дизритмия основного ритма. Если по нативной ЭЭГ можно лишь констатировать факт изменчивости основного ритма, то на спектрограммах и визуально, и количественно доступно определить за счет каких частотных компонентов это происходит. Применение спектрального анализа с этой целью показало, что основной ритм зачастую неоднороден. Оказалось, что для здоровых людей более характерен относительно узкий диапазон альфа-ритма. При тех или иных заболеваниях ЦНС визуально удовлетворительная корковая ритмика на нативных ЭЭГ содержит или расширенный диапазон основного ритма, или наличие двух и более независимых пиков в пределах одного частотного диапазона. Особенно это наглядно, когда максимальные значения мощности разных пиков альфа-ритма приходятся на различные группы отведений: один пик доминирует, например, в центральных или передних отделах (хотя присутствует и в задних), второй, как правило, — в затылочной области.
Что касается роли спектрального анализа в оценке активности волн дельта- и тета-диапазонов, то на сегодняшний день она ниже, чем альфа-активности, хотя значимость ее не меньше. Для этих видов биоэлектрической активности существенными характеристиками визуальной оценки являются их локализация, распространенность, устойчивость от эпохи к эпохе. Особенно это относится к тета-диапазону, учитывая высокое участие этих волн в формировании вспышек.
Условия применения спектрального анализа мощности ЭЭГ
Конфигурация кривых спектра мощности не постоянная «картинка» при любых условиях, а результат расчета, в определенной степени зависящий от алгоритма обработки. Это только абсолютный дилетант полагает, что «магическое» словосочетание «математический расчет» — это Эверест точности. Полное заблуждение. Конфигурация кривой спектра мощности зависит от ряда режимных величин. Назовем основные: 1) частота дискретизации усилителя ЭЭГ (в обычных приборах она колеблется от 120 до 500 Гц); 2) суммарная длина эпох ЭЭГ, выбранных для анализа (она может колебаться от 10 с до 90 мин и более в зависимости от поставленных задач); 3) количество выбранных точек для быстрого преобразования Фурье (обычно точки 256,512,1024, 2048, 4096 и т. д„ которые выбираются не произвольно, а с учетом тактовой частоты усилителя и длины эпохи анализа, а также примененного коэффициента сглаживания). Во многих программных продуктах все эти режимные величины представляют «кота в мешке», и алгоритмы настройки оптимального варианта расчетов не всегда ясны. При этом надо четко понимать, что конфигурация графиков спектра мощности чрезвычайно зависит от каждого из вышеперечисленных параметров (рис. 2, 3). Так, опытным путем установлено, что в большинстве случаев при тактовой частоте усилителя 500 Гц при суммарной длительности эпохи не менее 30 с оптимальной частотой быстрого преобразования Фурье (БПФ) является значение 4096 точек.

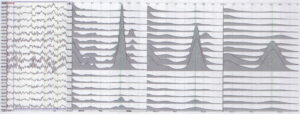
Спектр мощности в отображении локальных изменений
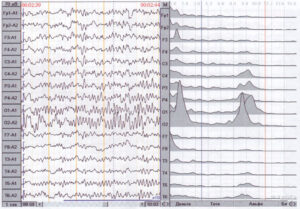
При визуальной оценке нативной ЭЭГ существенные изменения в виде локального преобладания, например медленных волн или асимметрии альфа-ритма по амплитуде, увидеть не представляет трудностей. При малой степени асимметрии, которая на нативной ЭЭГ не выявляется или только подозревается, спектральный анализ мощности на разных участках ЭЭГ одного исследования дает разброс попеременного преобладания сторон до 25 %. Из этого следует, что поиск мини-асимметрии нецелесообразен. Более того, небольшая асимметрия по альфа-ритму вообще физиологична и не имеет какого-либо диагностического смысла. Асимметрия выраженности альфа-ритма как признак полезна при ее очевидности. В количественном выражении асимметрия существенна, если разница между левой и правой стороной достигает 50 % мощности. Следует помнить, что выраженность асимметрии альфа-волн на нативной ЭЭГ всегда смотрится слабее, чем на спектрах мощности, так как мощность — это квадрат амплитуды.
Гораздо информативнее диагностировать асимметрию альфа-ритма по частоте. Заметить в нативной ЭЭГ замедление альфа-ритма на 1 Гц и тем более в полгерца в затылочной области одного из полушарий практически нет возможности. При построении графиков спектра мощности это видно невооруженным глазом (рис. 4).
Применение спектрального метода анализа
Причины широкого применения спектральный метод анализа:
- амплитудно-частотные характеристики ЭЭГ наиболее информативны для исследования текущего функционального состояния ЦНС;
- спектральные характеристики ЭЭГ поддаются математической и статистической обработке и потенциально могут дать эффективные методы анализа ЭЭГ, которые невозможно получить при традиционных методиках.
Концепция доказательной медицины включает требование научной обоснованности медицинских данных и их анализа. Количественный анализ и картирование ЭЭГ при помощи компьютерных систем позволяет внедрить математические и статистические методы обработки ЭЭГ не только в научно-исследовательскую, но и в клиническую практику, не прибегая к большим затратам.
В отличие от традиционных бумажных электроэнцефалографов компьютерные ЭЭГ-системы запоминают ЭЭГ-сигнал в памяти компьютера в оцифрованном виде, что позволяет не только распечатать ЭЭГ на принтере в привычном виде для визуального анализа, но и подвергнуть различным видам анализа, требующим больших компьютерных вычислений. Непрерывный аналоговый сигнал ЭЭГ преобразуется в оцифрованный вид при помощи аналогово-цифрового преобразователя, при этом частота оцифровки, т.е. количество измеренных через равные промежутки времени значений сигнала в секунду, зависит от типа предполагаемой обработки. Для фоновой ЭЭГ частота оцифровки обычно составляет не менее 100-200 Гц, для вызванных потенциалов может быть значительно больше. Точность преобразования «аналог- число» составляет не менее 3-4 отсчетов аналогово-цифрового преобразователя на 1 мкВ, для чего разрядность аналогово-цифрового преобразователя должна быть не менее 12 бит.
Частотный анализ предполагает изучение распределения какого-либо параметра ЭЭГ в зависимости от частоты. В первую очередь интерес представляет мощность для частотных составляющих ЭЭГ. Для измерения мощности в заданной частотной полосе во временной области необходимо отфильтровать достаточно большой участок ЭЭГ и вычислить средний квадрат значений амплитуды ЭЭГ. Таким образом, получаем мощность ЭЭГ (микровольты в квадрате) на заданном диапазоне частот, средняя амплитуда вычисляется через квадратный корень от мощности. Совокупность значений вычисленных таким образом амплитуды и мощности для всего частотного диапазона образует амплитудный спектр и спектр мощности соответственно. Для непрерывного (аналогового) сигнала можно получить непрерывный спектр значений амплитуды, в этом случае вычисляется спектральная плотность мощности с размерностью микровольт в квадрате/Герц, а мощность на заданном диапазоне вычисляется через интегрирование спектральной плотности мощности в заданных частотных границах. До широкого внедрения компьютеров использовали аналоговое оборудование: автоматические гармонические анализаторы ЭЭГ (Baldock, Walter, 1946), анализаторы с полосовой фильтрацией (Morris, Dave, 1953; Кожевников, 1953), аналоговые вычислительные машины (Lowenberg, McCullough, 1963) и пр.
При количественном анализе под словами «амплитуда ЭЭГ» подразумевается амплитуда не от пика до пика, как при традиционном визуальном анализе, а от пика до изолинии, т.е. нуле калибровочного сигнала. Спектральная амплитуда представляет собой усредненное значение на рассматриваемом временном интервале, в отличие от визуального анализа, где выборочно выбираются участки ЭЭГ с наиболее выраженным ритмом. По этим причинам спектральная амплитуда будет в 5-7 раз меньше, чем амплитуда в традиционном анализе.
В настоящее время для частотного анализа применяют, как правило, спектральный анализ. Математической основой спектрального анализа является преобразование Фурье исходных ЭЭГ-данных, которые рассматриваются как случайный процесс. Методов вычисления оценок спектров насчитывается не менее десятка, вариантов вычислительных процедур тоже достаточно много; какой-либо стандартной методики вычисления спектров не существует. На спектральную оценку могут влиять и допущения относительно исходных данных, и метод усреднения, и алгоритм вычисления и прочие обстоятельства, делающие спектральный анализ достаточно субъективным. На практике в большинстве случаев используется метод Кули и Тьюки – расчет спектра прямым дискретным преобразованием Фурье с использованием алгоритма быстрого преобразования Фурье. Реже используется вычисление спектров через преобразование Фурье корреляционной функции.
Так как ЭЭГ-сигнал представлен в системе дискретных равноотстоящих N точек (отсчетах АЦП) на заданном участке ЭЭГ (сегменте) с эпохой анализа (длительностью сегмента) T, при помощи дискретного преобразования Фурье (ДПФ) можно получить дискретный спектр, состоящий из N/2 гармоник (синусоидальных сигналов разной частоты, амплитуды и фазы) с равноотстоящими частотами с шагом 1/T. Амплитудный спектр и спектр мощности представлен амплитудой и мощностью этих гармоник соответственно. Для получения мощности на частотной полосе, превышающей шаг в спектральной области (1/T в Гц), нужно просуммировать мощности всех гармоник внутри этой полосы. Общая спектральная мощность должна быть равна мощности во временной области (т.е. средний квадрат исходного ЭЭГ-сигнала). Спектр, полученный на одной эпохе, иногда называют выборочным спектром. Выборочный спектр является статистически несостоятельным, так как среднеквадратичная ошибка сравнима по величине со средним значением самой оценки спектральной мощности.
Для получения статистически состоятельной оценки спектра используют следующие методики усреднения: по соседним частотам – метод Даньелла (Daniell), по непересекающимся эпохам – метод Бартлетта (Bartlett), по перекрывающимся эпохам – метод Уэлча (Welch). На практике длину эпохи анализа часто устанавливают равной 4-5 с, общая длина анализируемых ЭЭГ-данных должна составлять не менее 20 с.
Кроме спектров по одному отведению ЭЭГ, можно также получить взаимные спектры двух отведений (каналов). Взаимная спектральная плотность есть комплексная величина Sn=Cn-ixQn, где действительная часть Cn называется синфазной составляющей, а мнимая часть Qn – квадратурной составляющей взаимной спектральной плотности. Синфазная составляющая Cn – отношение среднего произведения двух процессов на n-й частоте к ширине n-й частоты. Квадратурная составляющая Qn – отношение среднего произведения процессов x(t) и y(t) на n-й частоте к ширине n-й частоты, причем один из процессов сдвинут относительно другого на π/2. Взаимную спектральную плотность также можно определить как преобразование Фурье кросс-корреляционной функции. Взаимные спектры также называют кросс-спектрами, а спектр по одному отведению – автоспектром.
На практике для описания взаимосвязи между отведениями используют комплексную функцию когерентности, которая вычисляется для каждой частоты или полосы (диапазона) частот через взаимную спектральную плотность мощности двух каналов делением на произведение автоспектров мощности. В этом случае иногда используют термин «когерентный анализ». Модуль функции КОГ на данной частоте меняется от нуля, когда нет статистической зависимости, до 1, когда есть полная статистическая зависимость. При ненулевой КОГ также можно измерить разность фаз на данной частоте между двумя отведениями и соответственно задержку по времени сигнала с одного отведения по отношению к другому.
Ряд спектральных показателей, такие как мощность, относительная мощность, когерентность, межполушарная асимметрия, рассматриваемые как случайные величины, могут быть приведены несложными математическими преобразованиями к нормальному распределению (Гаусса), что существенно упрощает их статистический анализ, так как многие виды статистической обработки, такие как критерий Стьюдента, ANOVA и прочие, требуют от данных нормального распределения. Скажем, логарифм от величины мощности для стандартных ритмов δ, θ, α, β является нормально распределенной случайной величиной для 20-секундных отрезках ЭЭГ. В этом случае можно подобрать контрольную группу одного пола и возраста, вычислить среднее по группе и стандартное отклонение спектрального показателя и сравнивать обследуемых с этими нормативными ЭЭГ-данными при помощи Z-критерия, в котором величина Z, определенная как степень отклонения от среднего по нормативной группе в единицах стандартного отклонения, не должна в норме превышать 2-3 S.D. Результаты такого анализа могут быть представлены в виде графиков, гистограмм и топографических карт. Использование набора подобных тестов для нормально распределенных спектральных параметров получило название «нейрометрика» (John E.R.).
Спектральный анализ ЭЭГ в программе Энцефалан
➥Основная статья: Руководство по анализу ЭЭГ в программе Энцефалан

Результаты спектрального анализа представляются в виде графиков спектральной плотности мощности, графиков амплитудных спектров, топографических карт, а также различных количественных показателей в табличном виде. Топографические карты в наглядной и сжатой форме показывают пространственное распределение различных параметров. Наиболее часто используются графики мощностных или амплитудных спектров, на которых по горизонтальной оси представлена частота (циклы/с или герцы), а по вертикальной оси — значения спектральной плотности мощности, характеризующие вклад (выраженность) каждой частотной составляющей в анализируемом фрагменте ЭЭГ. На графиках спектральной плотности мощности видно реальное частотное распределение мощности ЭЭГ-сигналов в каждом отведении (размерность — мкВ2/Гц) (Рис. 1.).
Это позволяет более точно оценить значения частот наиболее явных компонентов сигналов как по доминирующему ритму, так и по менее выраженным ритмам, оценить регулярность по частоте (по степени размазанности основных пиков), определить количественные показатели мощностной и частотной асимметрии (по амплитуде пиков и значениям соответствующих частот), оценить реакцию усвоения ритма световых мельканий или звуковых стимулов на основной частоте и на ее гармониках (по сопоставлению динамики изменения мощностных характеристик на этих частотах в фоновой записи и во время ритмической стимуляции), проанализировать структуру спектра для полиритмичной ЭЭГ. Мощностной спектр используется чаще, чем амплитудный, потому что он более нагляден, выражается в действительных значениях, а не мнимых. Значения амплитуд в амплитудном спектре, показываемые для каждой конкретной частоты (частотного отсчета с шагом порядка 0,25 Гц), значительно меньше амплитуд ЭЭГ, оцениваемых при визуальном анализе той же кривой. Это объясняется тем, что компьютерный анализ дает среднеквадратическое значение, составляющее около 35% от значения амплитуды при измерении от пика до пика. Кроме того, при визуальной оценке амплитуды реальной ЭЭГ традиционно берут значения, близкие к максимальным по тем отведениям, в которых активность данного ритма наиболее выражена. Необходимо отметить, что нерегулярность по частоте при визуальном анализе учитывается отдельно, а амплитуда берется общая по всему частотному диапазону ритма. Амплитудный же спектр выдает объективную информацию о вкладе каждой частотной составляющей. Это обстоятельство необходимо учитывать при оценке численных значений на графиках амплитудного спектра, однако это не должно смущать врача, поскольку напрямую сопоставлять значение амплитудного спектра конкретного частотного отсчета с амплитудой ритма, в обычном его понимании, в общем случае нельзя. При автоматическом формировании описания энцефалограммы определение амплитуд ритмов происходит по другим принципам, поэтому расхождение с визуальной оценкой получается минимальным.
Спектральные характеристики
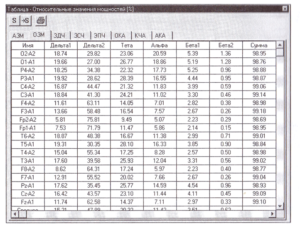
Количественные показатели рассчитанных спектральных характеристик ЭЭГ выдаются на экран и на печать в табличном виде. Для спектра мощности формируются следующие спектральные характеристики:
- Абсолютные значения мощностей (АЗМ) [мкВ2] — площадь под соответствующим участком спектрограммы по выбранным частотным диапазонам.
- Относительные значения мощностей (ОЗМ) или индексы мощности [%] — отношение площади под соответствующим участком спектрограммы к суммарной площади по выбранным частотным диапазонам, умноженное на 100%.
- Значения доминирующих частот (ЗДЧ) по выбранным частотным диапазонам [Гц] — частоты, соответствующие максимуму на участке спектрограммы.
- Значения средневзвешенных частот (ЗСЧ) по выбранным частотным диапазонам [Гц]. ЗСЧ рассчитывается следующим образом: среднее значение частоты каждого частотного дискрета умножается на значение этого дискрета, суммируются все произведения, относящиеся к данному частотному диапазону. После чего полученное значение делится на значение площади под кривой частотного диапазона. В этой таблице визуализируются также средние значения средневзвешенных частот по каждому из частотных диапазонов по всем отведениям.
- Абсолютный коэффициент асимметрии (АКА) [%] — определяется как отношение разности по модулю между значениями мощности по симметричным отведениям к максимальному значению.
- Относительный коэффициент асимметрии (ОКА) [%] — определяется как отношение разности по модулю между значениями мощности по симметричным отведениям к среднему значению по данному частотному диапазону по всем отведениям (кроме центрального ряда).
- Коэффициент частотной асимметрии (КЧА) [%] — определяется как отношение суммы модулей разности между нормированными значениями мощности по симметричным отведениям к сумме этих же значений.
- Эффективная полоса частот (ЭПЧ) [Гц] — в определенной степени характеризует регулярность по частоте и вычисляется как отношение спектра мощности выделенного частотного диапазона к максимальному значению спектральной плотности мощности в этом частотном диапазоне.
Пример таблицы спектральных характеристик ЭЭГ, изображенной на Рис. 2, приведен на Рис. 3.
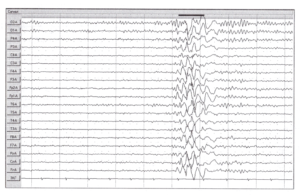
Примеры использования спектрального анализа
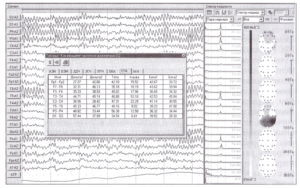
Рассмотрим примеры использования режима спектрального анализа для реальных ЭЭГ. На Рис. 4 в линейном варианте представления результатов показан фрагмент ЭЭГ с графиками спектральной плотности мощности и топографическими картами, характеризующими этот фрагмент ЭЭГ. Видно, что, наряду с мощностной асимметрией, существует и явная частотная асимметрия. В таблице «Коэффициент частотной асимметрии» отражено, что между отведениями Т3-Т4 коэффициент частотной асимметрии по альфа-диапазону составил 53,1 %, в левом полушарии доминирующая частота — 10,0 Гц, в правом полушарии — 10,5 Гц. Однако на исходных сигналах тяжело оценить наличие и степень частотной асимметрии.
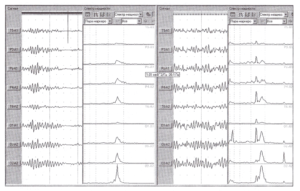
Использование спектрального анализа может быть полезным для оценки изменений ЭЭГ при проведении фото- или фоностимуляции. Навязывание ритма не всегда происходит на частоте стимуляции, достаточно часто это может происходить на кратных гармониках. Чем на большем количестве частот производится усвоение ритма, тем тяжелее это распознается при визуальном анализе ЭЭГ.
На Рис. 5 представлены графики спектральной плотности мощности фоновой записи ЭЭГ и фотостимуляции. В исходном фоновом состоянии преобладал альфа-ритм с доминирующей частотой — 11 Гц. При ритмической фотостимуляции с частотой 10 Гц в теменно-затылочных отведениях появились пики на кратных частотах 10 и 20 Гц, то есть произошло усвоение ритма на тех гармониках, которые соответствуют физиологически нормальным для здорового человека ритмам. На Рис. 6 представлена псевдотрехмерная динамика результатов анализа, которая позволяет оценить изменения спектральных характеристик ЭЭГ при проведении функциональных проб как во всех отведениях, так и в отдельно взятом отведении (Рис. 7.).


Средства спектрального анализа являются неотъемлемой частью количественного анализа ЭЭГ и дают врачу дополнительную информацию, которую при обычном визуальном анализе ЭЭГ трудно получить. Спектральная форма представления процесса наиболее близка к принятой в электроэнцефалографии оценке ЭЭГ по частотному характеру, который, по мнению большинства исследователей, считается наиболее информативным.
Использование спектрограмм и количественных спектральных показателей позволяет снизить степень субъективности при описании и интерпретации ЭЭГ, например, при оценке наличия и выраженности амплитудной и частотной асимметрии, регулярности и однородности ритма, при анализе структуры частотных составляющих, их выраженности в различных областях мозга, степени усвоения ритмических воздействий различной модальности, а также при выявлении фокальных проявлений и др. Результаты спектрального анализа могут быть использованы для донозологической диагностики. Они позволяют выявлять тенденции перестройки ритмики в процессе как медикаментозной, так и немедикаментозной терапии, например, при реабилитационных процедурах на основе биоуправления с биологической обратной связью, задолго до того, как это будет видно при обычном визуальном анализе нативной ЭЭГ. Спектральный анализ ЭЭГ имеет большое практическое значение в нейрофизиологии, особенно при мониторинге больных, длительное время находящихся в коматозном состоянии, при обследовании больных с сосудистыми заболеваниями головного мозга, при эпилепсии.
Цифровые методы спектрального оценивания сигналов
При исследовании сигналов часто используются методы спектрального анализа, позволяющие получить численные оценки частотного состава сигнала. Спектральный анализ основан на частотном подходе к анализу сигналов.
Наиболее распространены методики спектрального анализа, основанные на дискретном преобразовании Фурье (ДПФ):
![]()
где х(n) — отсчеты дискретного сигнала, N — число отсчетов, а k = 0, 1, …, N – 1 — номера частотных составляющих разложения. Для ускорения расчета применяют алгоритмы быстрого преобразования Фурье (БПФ)123.
В результате выполнения процедуры ДПФ получается ровно N значений комплексных чисел, описывающих гармонические колебания (синусоиды) с частотами 0, f0, 2f0, 3f0…..(N – 1)fо, где f0 = fД/N-основная частота преобразования (fд частота дискретизации сигнала). Амплитуда и фазовый сдвиг каждой из синусоид определяются как модуль и аргумент соответствующего комплексного элемента разложения.
По полученному разложению исходный сигнал может быть полностью восстановлен (в точках взятия отсчетов) с использованием процедуры обратного дискретного преобразования Фурье.
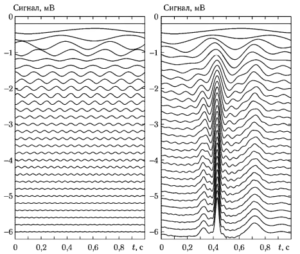
Па рис. 1 иллюстрируется процесс реконструкции фрагмента ЭКГ при помощи синусоид, определяемых значениями элементов ДПФ. Левые графики показывают синусоиды со значениями частот 0, f0, 2f0, 3f0…..(N – 1)fо. а правые — этапы реконструкции сигнала с помощью этих синусоид. Рисунок позволяет проследить, как суммирование синусоидальных составляющих дает возможность получить описание кривой практически произвольной формы.
Спектральное оценивание на основе дискретного преобразования Фурье
В случае использования алгоритма БПФ для получения спектральных оценок возможны два основных варианта: расчет БПФ для всего фрагмента сигнала целиком (периодограммный метод) или использование усреднения спектров, рассчитанных по перекрывающимся фрагментам сигнала (метод Уэлча).
При использовании периодограммного метода выполняется следующая последовательность процедур45:
- Удаление из сигнала среднего значения (или линейного тренда) с целью устранения постоянной составляющей.
- Умножение сигнала на сглаживающее окно (см. далее) для уменьшения спектральной утечки, вызываемой разрывами на краях анализируемого фрагмента, возникающими при его периодическом продолжении.
- Дополнение фрагмента сигнала нулями до размера, соответствующего какой-либо целой степени числа «2», что позволяет далее использовать алгоритм БПФ.
- Расчет дискретного преобразования Фурье с помощью алгоритма БПФ.
- Расчет спектральной плотности мощности (СПМ):
![]()
где fд частота дискретизации, fk = klΔf = kfд/N, k= 0, 1,2, … …,N/2, а X(fk) и p(fk) — соответственно значения компонентов разложения по Фурье и СПМ для частот fk.
- Умножение СПМ на корректирующий коэффициент, учитывающий потери мощности при использовании сглаживающего окна:
![]()
где Nw — размер окна в отсчетах, a w(n) — отсчеты оконной функции.
- Умножение СПМ на корректирующий коэффициент, учитывающий потерн мощности при дополнении нулями:
kо = N/No,
где No — число отсчетов фрагмента сигнала до дополнения нулями.
При использовании метода Уэлча67 исходный сигнал разбивается на сегменты, для каждого из которых спектральная оценка рассчитывается при помощи описанной выше процедуры. Далее полученные оценки усредняются по соответствующим частотам. Оценки спектральной плотности мощности, полученные с помощью метода Уэлча, отличаются большей статистической устойчивостью по сравнению с простым периодограммным методом.
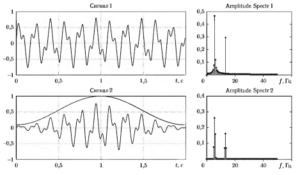
Из-за того что при использовании ДПФ неявно предполагается бесконечное периодическое продолжение анализируемого сигнала, в получаемом спектре может наблюдаться эффект, называемый спектральной утечкой, который проявляется в «растекании» мощности спектральных составляющих по диапазону частот. Этот эффект может быть снижен за счет применения так называемых сглаживающих окон. Под последними понимаются функции, имеющие на краях близкие к нулю значения, которые плавно возрастают до единицы в средней части функции. На рис. 2 демонстрируется эффект спектральной утечки и результат ее снижения с использованием сглаживающего окна. 11а левом верхнем графике показан фрагмент сигнала, представляющего собой смесь двух синусоид (с частотами 7 Гц и 13 Гц). Справа сверху показан амплитудный спектр этого сигнала, где для составляющей с частотой 7 Гц наблюдается спектральная утечка. На нижнем левом графике показаны сглаживающая функция и сигнал, полученный в результате умножения исходного сигнала на эту функцию. Как можно видеть, значения последней функции приближаются к нулевым на концах фрагмента. Правый нижний график содержит амплитудный спектр полученного сигнала, в котором эффект спектральной утечки существенно снижен. Однако следует иметь в виду, что применение сглаживающих окон, хоть и снижает спектральную утечку, но приводит в то же время к ухудшению спектрального разрешения, т. е. способности спектра к различению близких по частоте составляющих.
Параметрические методы спектрального оценивания
Альтернативный подход к расчету спектральных оценок реализуется с использованием так называемых параметрических методов. Наиболее распространенные из них основаны на модели авторегрессии (ЛР), описываемой уравнением:
![]()
где х(n) — отсчеты процесса авторегрессии, w(n) — отсчеты возбуждающего белого шума, аk — коэффициенты модели, а р— порядок модели.
Если по последовательности отсчетов некоторого анализируемого сигнала удастся найти набор коэффициентов авторегрессии ад. и получить оценку дисперсии возбуждающего белого шума pw, то оценка спектральной плотности мощности (СПМ) данного сигнала будет определяться выражением89:
![]()
где Т = 1/fд период дискретизации сигнала, а f частота соответствующего значения СПМ.
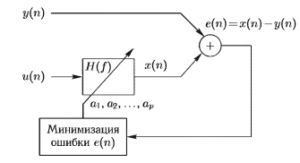
Идея авторегрессионного метода иллюстрируется на рис. 3. Пусть требуется оценить спектральную плотность мощности некоторого наблюдаемого дискретного сигнала у(n). Подадим на вход рекурсивного цифрового фильтра, имеющего набор коэффициентов a1, a2, …, ap и передаточную функцию H(f), воздействие г/(n) в виде отсчетов белого шума (абсолютно случайного сигнала). Тогда в случае. если удастся так подобрать коэффициенты фильтра, что средняя энергия ошибки е(n) окажется минимальной, можно считать, что передаточная функция фильтра H(f) (с точностью до множителя pw представляющего собой оценку дисперсии возбуждающего белого шума u(n)) является оценкой спектральной плотности мощности сигнала у(n).
Разработан целый ряд алгоритмов оценки параметров авторегрессии (коэффициентов a1, a2, …, ap и параметра pw), из которых наиболее известны следующие четыре:
- автокорреляционный метод Юла-Уоркера;
- метод максимальной энтропии Берга;
- ковариационный метод;
- модифицированный ковариационный метод.
Из перечисленных алгоритмов наилучшие результаты дают последние два, основанные на методах линейного предсказания. В то же время эти методы наиболее сложны в вычислительном отношении.
Процедура получения спектральных оценок с помощью авторегрессионных методов может быть описана следующей последовательностью этапов:
- Удаление из сигнала среднего значения (или линейного тренда) с целью устранения постоянной составляющей.
- Выбор порядка модели р.
- Оценивание параметров АР модели («), a1, a2, …, ap иpw).
- Вычисление оценки СПМ P(f).
- Анализ полученных результатов и при необходимости выбор нового значения порядка р (т. е. переход обратно к шагу 2).
Последний из этапов выполняется до тех пор, пока не будет достигнут приемлемый компромисс между частотным разрешением СПМ и дисперсией получаемых спектральных оценок10. Чем больше выбранная величина порядка р, тем выше разрешение получаемой оценки СПМ (т. е. возможность различения близких по частоте составляющих), но при этом большим оказывается и разброс спектральных оценок, т. с. статистическая устойчивость результатов анализа снижается. Как видим, применение данных методов предполагает необходимость контроля результатов человеком-исследователем, что является одним из главных недостатков параметрических методов.
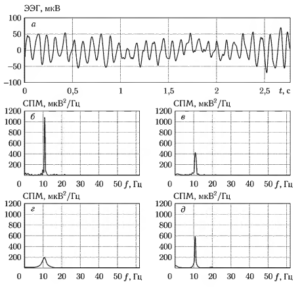
На рис. 4 показан фрагмент сигнала ЭЭГ и примеры оценок СПМ, рассчитанных альтернативными методами. Как можно видеть, полученные оценки СПМ существенно отличаются друг от друга. В то же время, на каждом из графиков отчетливо виден пик на частоте чуть выше 10 Гц, соответствующий a-ритму. Необходимо отметить, что хотя высота пиков на графиках СПМ различна, суммарная мощность, равная площади под кривой СПМ, во всех случаях одна и та же.
В табл. 1 дана сравнительная характеристика методов на основе ДПФ и параметрических методов. В практических задачах выбор конкретного метода расчета спектральных оценок необходимо осуществлять, учитывая как частотные свойства сигнала, так и конечные цели и условия анализа сигнала.
Таблица 1. Сравнение альтернативных методов спектрального анализа
| Методы спектрального анализа | ||
| Классические (на основе ДПФ) | Параметрические (авторегрессионные) | |
| Достоинства | Математическая простота. Обратимость ДПФ. | Более реалистические, чем в случае классических методов, предположения о сигнале за пределами анализируемого фрагмента. Возможность анализа спектра по относительно коротким фрагментам сигнала. |
| Недостатки | Появление спектральной утечки вследствие предполагаемой периодичности сигнала (т. е. нереалистического предположения о сигнале за пределами анализируемого фрагмента). Необходимость наличия относительно продолжительного фрагмента сигнала. | Математическая сложность. Необратимость спектра. Необходимость субъективного выбора порядка АР модели. |
Взаимная спектральная плотность мощности и функция когерентности
Взаимосвязь колебательных процессов, присутствующих в двух одновременно наблюдаемых сигналах, наиболее полно позволяет отразить их взаимный спектр, который содержит информацию как о мощности совместных колебаний, так и о фазовых сдвигах между колебаниями с одинаковыми частотами1112. Функция взаимной спектраль ной плотности мощности (ВСПМ) может быть получена как преобразование Фурье от взаимной корреляционной функции (ВКФ) двух сигналов:
pxy(f) = FT|Сху(τ)| = X* (f) Y(f)
где pxy(f) — значение ВСПМ сигналов x и у для частотыf, Сху(τ) — ВКФ для временного сдвига τ, а X(f) и Y(f) преобразования Фурье для соответствующих сигналов.
На практике при цифровом анализе сигналов оценка ВСПМ может быть получена различными способами, из которых наиболее известны следующие ]:
- Непосредственное вычисление ВСПМ по ДПФ двух синхронно снятых дискретных выборок сигналов x(n) и у(п), где n = 0, 1, …, N-1.
Если ДПФ сигналов определены как
![]() , k = 0, …. , N-1
, k = 0, …. , N-1
![]() , k = 0, …. , N-1
, k = 0, …. , N-1
то оценка ВСПМ может быть рассчитана как
![]() , k = 0, …. , N-1
, k = 0, …. , N-1
- Получение оценки ВСПМ как ДПФ от оценки ВКФ.
В этом случае сначала вычисляется смещенная оценка взаимной корреляционной функции двух сигналов:
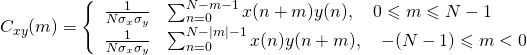
где m — значение сдвига, а σх и σу — стандартные отклонения соответствующих сигналов. Тогда оценка ВСПМ может быть рассчитана по формуле:
![]() , k = 0, …. , 2(N-1)
, k = 0, …. , 2(N-1)
- Расчет оценки ВСПМ с использованием одного из распростра ценных методов практического спектрального анализа — периодограммного метода Уэлча, который включает следующие этапы:
- Разбиение анализируемых фрагментов на перекрывающиеся сегменты одинаковой длительности.
- Вычисление ВСПМ для каждого из сегментов.
- Усреднение ВСПМ по всем сегментам.
Далее для любого из трех методов модуль ВСПМ и ее аргумент (взаимный фазовый спектр, ВФС) могут быть рассчитаны по формулам
![]()
![]()
Полученное значение |Рxy(k)| имеет размерность произведения размерностей обоих сигналов, а значение ∠Pxy(k) выражается в радианах. Обычно бывает удобнее представлять фазовый сдвиг в градусах:
∠Pxy0(k)= ∠Pxy(k) 180°/π.
Временной сдвиг между сигналами для какой-либо определенной частоты fk = kfд/N (где fд — частота дискретизации, а N — число элементов ДПФ) может быть определен как
![]()
если ВФС выражен в радианах, или
![]()
если ВФС выражен в градусах.
Важно отметить, что порядок вычисления взаимного спектра влияет на знак получаемого фазового сдвига. Положительным значениям фазы будет соответствовать запаздывание первого их сигналов относительно второго и наоборот.
Помимо ВСПМ часто рассматривается функция когерентности, определяемая выражением :
![]()
Функция когерентности представляет собой нормированный вариант ВСПМ, и ее модуль может принимать значения не более единицы. Эго может оказаться удобным для оценки относительной степени взаимосвязанности двух процессов на определенной частоте.
В разделе 4.1 представлен пример применения ВСПМ для решения задачи совместного анализа сигналов сердечного ритма и артериального давления.
Применение методов спектрального оценивания при анализе биомедицинских сигналов
Методы спектрального анализа находят широкое применение для исследования частотного состава таких биомедицинских сигналов как
электрокардиограмма, электроэнцефалограмма, электромиограмма, фонокардиограмма и ряда других1314 1516.
Рассмотрим пример использования данных методов для анализа ЭЭГ, являющейся записью электрических потенциалов мозга, снимаемых с поверхности головы человека. Выделяют четыре основных ритма ЭЭГ:
- δ (дельта) с частотой 0,5-3 Гц и амплитудой 40 300 мкВ;
- θ (тета) с частотой 4-6 Гц и амплитудой 40-300 мкВ;
- α (альфа) с частотой 8-13 Гц и амплитудой до 100 мкВ;
- β (бета) с частотой 14 40 Гц и амплитудой до 15 мкВ.
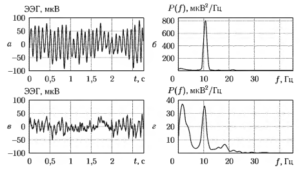
Рассчитав спектральную оценку сигнала ЭЭГ, можно получить количественные характеристики каждого из ритмов в отдельности. На рис. 5 показан пример получения спектральных оценок для двух синхронно снятых каналов ЭЭГ человека. Справа приведены графики фрагментов сигналов, а слева графики рассчитанных по ним оценок СПМ. Верхние графики соответствуют сигналам с лобной части головы, а нижние — с затылочной. На верхнем правом графике (б) отчетливо виден пик, соответствующий выраженному альфа ритму с частотой около 10 Гц. Этот ритм наблюдается у здоровых людей в состоянии покоя с закрытыми глазами и наиболее сильно проявляется в затылочных отведениях. В то же время в спектре ЭЭГ, снятой с электрода, размещенного в лобной части головы, вклад альфа-ритма на порядок меньше (график г).
Для получения количественных оценок частотных свойств ЭЭГ по рассчитанной спектральной плотности мощности для заданного частотного диапазона ЭЭГ вычисляются следующие основные численные показатели17:
- Aср — средняя амплитуда;
- Аmах — максимальная амплитуда;
- Fcр — средневзвешенная частота;
- Fmах — частота максимальной амплитуды спектра.
Если общее число элементов спектрального разложения равняется N, а частота дискретизации fд, то шаг спектра по оси частот составит Δf = fд/N. При этом частота, соответствующая элементу спектра с номером k, будет определяться выражением fk = k•Δf, а соответствующее значение СПМ может быть обозначено как P(fk). Если задать границы какого-либо частотного диапазона ЭЭГ номерами соответствующих составляющих спектра k1 и k2, то первые три из перечисленных выше спектральных показателей могут быть рассчитаны по формулам:
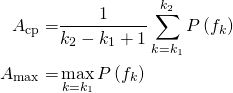
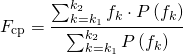
Показатель Fmах определяется как частота, соответствующая значению Аmах.
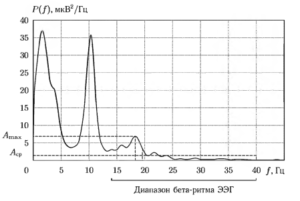
На рис. 6 иллюстрируется смысл описанных спектральных показателей для частотного диапазона, соответствующего бета-ритму ЭЭГ (14-40 Гц).
Одним из применений частотного анализа ЭЭГ является также автоматический контроль глубины анестезии в ходе хирургических операций.
При автоматическом анализе ЭКГ спектральные методы используются для решения целого ряда диагностических задач, в частности: обнаружение опасных аритмий по спектральному описанию электро-кардиосигпала, классификация форм желудочковых комплексов ЭКГ, анализ вариабельности сердечного ритма.
Литературные источники
- Александров М. В., Иванов Л. Б., Лытаев С. А. [и др.]. Электроэнцефалография : руководство / под ред. М. В. Александрова. — 3-е изд., перераб. и доп. — СПб.: СпецЛит, 2020. — 224 с.
- Александров М. В., Иванов Л. Б., Лытаев С. А. [и др.]. Общая электроэнцефалография / под ред. М. В. Александрова. — СПб.: Стратегия будущего, 2017. — 128 с.
- Бреже М. Электрическая активность нервной системы : пер. с англ. — М. : Мир, 1979. — 264 с.
- Гнездицкий В. В. Обратная задача ЭЭГ и клиническая электроэнцефалография. — М.: МЕДпресс-информ, 2004. — 624 с.
- Зенков Л. Р. Клиническая эпилептология (с элементами нейрофизиологии). – М.: МИА, 2002. – 416 с.
- Русинов В. С., Майоргик В. Е., Гриндель О. М. [и др.]. Клиническая электроэнцефалография / под ред. В. С. Русинова. — М.: Медицина, 1973. — 339 с.
- Niedermeyer E., Lopes da Silwa F. Electroencephalography. Basis, principles, clinical applications related fields. — Philadelphia-Baltimore — NY: Lippincott Williams & Wilkins, 2005. – 1309 p.
Footnotes
- Аифичер Э. С.. Джервис Б. У. Цифровая обработка сигналов: практический подход / Пер. с англ. — М.: ИД «Вильямс», 2004. — 992 с.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
- Микрокомпьютерные медицинские системы: Проектирование и применение / Под ред. У.Томпкинса, Дж. Уэбстера: Пер. с англ. — М.: Мир, 1983. – 544 с.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
- Рангайян Р. М. Анализ биомедицинских сигналов / Пер. с англ. A. II. Калиниченко; под ред. Л. П. Немирно. — М.: Физматлит, 2007. — 440 с.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
- Рангайян Р. М. Анализ биомедицинских сигналов / Пер. с англ. A. II. Калиниченко; под ред. Л. П. Немирно. — М.: Физматлит, 2007. — 440 с.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
- Рангайян Р. М. Анализ биомедицинских сигналов / Пер. с англ. A. II. Калиниченко; под ред. Л. П. Немирно. — М.: Физматлит, 2007. — 440 с.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
- Дженкинс, Г. Спектральный анализ и его приложения / Г. Дженкинс, Д. Ватте; пер. с англ. — М.. Мир, 1971. — 316 с.
- Рангайян Р. М. Анализ биомедицинских сигналов / Пер. с англ. A. II. Калиниченко; под ред. Л. П. Немирно. — М.: Физматлит, 2007. — 440 с.
- Аифичер Э. С.. Джервис Б. У. Цифровая обработка сигналов: практический подход / Пер. с англ. — М.: ИД «Вильямс», 2004. — 992 с.
- Дюк В., Эмануэль В. Информационные технологии в медико-биологических исследованиях. СПб. «Питер», 2003. — 528 стр.
- Микрокомпьютерные медицинские системы: Проектирование и применение / Под ред. У.Томпкинса, Дж. Уэбстера: Пер. с англ. — М.: Мир, 1983. – 544 с.
- Рангайян Р. М. Анализ биомедицинских сигналов / Пер. с англ. A. II. Калиниченко; под ред. Л. П. Немирно. — М.: Физматлит, 2007. — 440 с.
- Дюк В., Эмануэль В. Информационные технологии в медико-биологических исследованиях. СПб. «Питер», 2003. — 528 стр.