Настоящий прорыв в исследованиях мембран клеток вызвал так называемый метод patch-clamp, который был создан на основе метода внутриклеточного диализа клеток, разработанного в 1976 г. в Институте физиологии им. А.А. Богомольца (Киев) под руководством акад. П.Г. Костюка12. Метод patch-clamp предложили в 1976 г. E. Neher и B. Sakmann3. И хотя в его основе лежал принцип исследования клеток методом диализа, предложенный метод отличался рядом технических модификаций и был крайне сложным. Однако уже в 1981 г., после публикаций O.P. Hamill и соавт.45, этот метод превратился в общедоступный, позволяющий проводить любые измерения на клеточном уровне. В настоящее время все электрофизиологические исследования мембран клеток производят при помощи данного метода.
Метод patch-clamp позволяет регистрировать на изолированных клетках их потенциалы, токи или одиночные ионные каналы посредством специальной стеклянной пипетки (patch-пипетки), напоминающей микроэлектрод, но имеющей сопротивление от 2 до 10 МОм в зависимости от типа исследуемых клеток. Кроме того, метод позволяет регистрировать ионные каналы с изолированного кусочка мембраны, который может быть расположен по отношению к отверстию пипетки либо внешней, либо внутренней стороной.
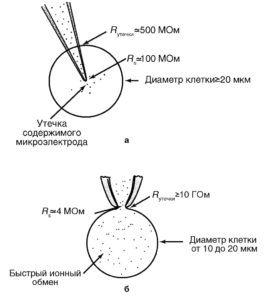
На рис. 1 показаны микроэлектрод и patch-пипетка и продемонстрированы их основные отличия.
По сравнению с методами микроэлектродной техники и классической фиксации потенциала применение пипетки имеет ряд положительных моментов. Во-первых, техническая поддержка метода позволяет при помощи одного прибора исследовать клетки как в режиме фиксации тока, так и в режиме фиксации потенциала. Во-вторых, метод patch-clamp позволяет изучать мелкие клетки без существенного повреждения их мембран, тогда как даже один микроэлектрод, а тем более – два, существенно повреждают мембрану. Далее, сопротивление утечки микроэлектрод-мембрана не превышает 500 МОм, а при использовании метода patch-clamp и, соответственно, patch-пипетки – более 10 ГОм, что существенно влияет на качество регистрации. Наконец, микроэлектроды имеют сопротивление, достигающее 100 МОм, а patch-пипетки – от 2 до 10 МОм, что позволяет не только качественно регистрировать потенциалы и токи клетки, но и вводить в клетки без особых проблем любые соединения.
Для исследований методом patch-clamp существует несколько практически одинаковых приборов, например BioLigic, Axopatch, List Elektronik, которые позволяют в режиме current-clamp (фиксация тока) регистрировать потенциалы клеток и осуществлять их электрическое раздражение, а в режиме voltage-clamp (фиксация потенциала) – измерять суммарные ионные токи клетки или токи через одиночные ионные каналы. Эти приборы комплектуются аналогово-цифровыми преобразователями, которые выполнены либо как отдельные приборы, либо как карты, инсталлирующиеся в персональный компьютер. Кроме того, в комплект поставки включены: программа для регистрации процессов во всех режимах работы и программа для обработки зарегистрированных процессов.
Поскольку практически все известные в настоящее время электрофизиологические результаты получены методом patch-clamp, мы подробно остановимся на ряде методических вопросов. Без их усвоения достаточно трудно достичь полного понимания полученных этим методом результатов.
Конфигурации patch-пипетка-мембрана
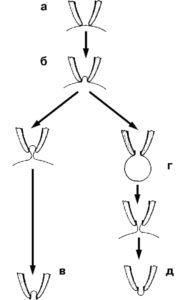
На рис. 2 показаны различные конфигурации patch-clamp по отношению к клетке или фрагменту ее мембраны. Сначала пипетку подводят вплотную к мембране изолированной клетки (см. рис. 2, а) и создают в ней небольшое отрицательное давление (см. рис. 2, б). Это приводит к тому, что мембрана плотно закупоривает отверстие пипетки, и формируется высокоомный контакт – конфигурация cell-attached или, иначе, переход пипетка-мембрана с сопротивлением утечки более 1 ГОм (так называемый giga-seal). После нормализации давления в пипетке конфигурация cell-attached близка к физиологической ситуации, поскольку зона мембраны, захваченная пипеткой, с внутренней стороны контактирует с внутриклеточной жидкостью, а с внешней стороны – со стандартным внеклеточным раствором, которым заполняют patch-пипетку. Эта конфигурация, с одной стороны, позволяет регистрировать одиночные ионные каналы под пипеткой, а с другой – является промежуточной для других конфигураций. Она позволяет изучать на одиночном канале роль вторичных мессенджеров, которые включаются через рецепторы плазматической мембраны.
Конфигурация cell-attached позволяет сформировать другую конфигурацию, называемую inside-out patch. К ее образованию приводит резкое отрывание пипетки от клетки (см. рис. 2, в), причем giga-seal не меняется. В этом случае на пипетке находится лишь фрагмент мембраны ( patch), внутренняя сторона которой смотрит в омывающий раствор перфузионной камеры, а внешняя контактирует с содержимым пипетки. Данную конфигурацию используют для изучения вклада соединений цитоплазмы в канальную активность.
Конфигурация cell-attached позволяет двумя путями (в зависимости от задач исследователя) сформировать конфигурацию, называемую whole-cell. В одном случае для ее получения в пипетку необходимо резко и одномоментно подать небольшое отрицательное давление, разрывающее мембрану под пипеткой и образующее низкоомный путь между внутренней средой клетки и раствором в пипетке. При этом в мембране возникает дырка, величина которой позволяет осуществлять обмен ионов и различных соединений между пипеткой и цитоплазмой (см. рис. 2, г). В другом случае низкоомный путь между внутренней средой клетки и раствором в пипетке формируется благодаря влиянию соединений, находящихся в пипетке и вызывающих образование в мембране пор, проницаемых для ионов, но не для молекул. Это перфоративный (perforated) patch. Антибиотики нистатин (nystatin) и амфотерицин Б (amphotericin B) используют в пипеточном растворе, чтобы образовать специфические поры на участке мембраны под пипеткой. Они пропускают через мембрану моновалентные катионы и анионы. Еще одно соединение – грамицидин (gramicidin) – помогает формировать каналы, проницаемые только для моновалентных катионов. Эта методика позволяет исследовать ионные токи, протекающие через мембрану, идентифицировать и вычленить их.
Конфигурация whole-cell позволяет сформировать еще один вариант конфигурации – outside-out patch (см. рис. 2, д). Медленное оттягивание пипетки от клетки заставляет мембрану растягиваться до тех пор, пока она не отделится от клетки и не сошьется.
Теперь ее внутренняя часть будет контактировать с раствором в пипетке, а внешняя – с омывающим раствором в перфузионной камере. Данную конфигурацию применяют для изучения вклада соединений внешней среды клетки в активность единичных каналов.
Рatch-пипетки
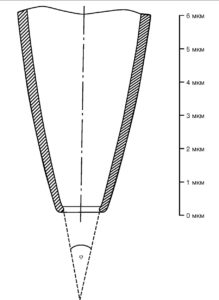
При всех конфигурациях patch-clamp используют patch-пипетки, основное различие которых в зависимости от задач экспериментатора заключается в их сопротивлении, т.е. в диаметре кончика patchпипетки. Patch-пипетки, кончик которых представлен на рис. 3, обычно вытягивают из стандартных коммерческих капилляров внешним диаметром 2 мм, содержащих один стеклянный филамент (например, GB200F-8P; Science Products GmbH).
Patch-пипетки изготавливают вытягиванием в две стадии, как это предложено Хэмиллом и соавт. (Hamill et а1., 1981). На первом этапе вытягивания patch-пипетки капилляр должен приобрести утончение диаметром 200-400 мкм в месте расположения спирали (в месте разогрева). На втором этапе диаметр уменьшается до 1-2 мкм, и в результате разрыва утончения получаются две patch-пипетки. Принцип вытягивания patch-пипеток не является критичным для дальнейшей работы, поэтому пригодны многие типы кузниц. Они должны иметь небольшую силу рывка, приспособление для остановки на первом этапе вытягивания и плавный точный режим нагрева спирали. Во многих лабораториях применяют так называемую кузницу Копфа (David Kopf Instruments, USA). Эта кузница имеет фиксированный сверху и подвижный снизу держатели для капилляра, поэтому две полученные patch-пипетки не являются идентичными; обычно используют только нижнюю patch-пипетку (при наличии горизонтальной программируемой кузницы можно использовать обе полученные пипетки, которые имеют после вытяжки одинаковые параметры). После первого этапа происходит автоматическое отключение нагрева спирали. Для реализации второго этапа вновь включают нагрев спирали, находящейся в центре утончения, и после разогрева стекла в результате разрыва утончения получаются две patch-пипетки.
Многие исследователи обычно оплавляют полученные patchпипетки. Patch-пипетку крепят на отдельном микроманипуляторе так, чтобы нагревательный элемент и patch-пипетку можно было перемещать независимо друг от друга. При оплавлении кончик patch-пипетки выдерживают в течение нескольких секунд на расстоянии 2-10 мкм от стеклянного покрытия нагревательного элемента. Обычно у неоплавленного электрода хорошо видно отверстие кончика. При оплавлении просвет становится невидимым. Размер кончика пипетки в этом случае оценивают путем пропускания воздуха через
patch-пипетку, кончик которой погружен в метанол. Для этого пипетку соединяют при помощи полиэтиленовой трубочки длиной 10 см со шприцем объемом 10 мл. Если к patch-пипетке приложить давление, то из ее кончика начнут выходить пузырьки воздуха, как только величина давления превысит поверхностное натяжение на границе фаз «воздух-метанол». Поскольку поверхностное натяжение обратно пропорционально радиусу кривизны, из кончиков с большим диаметром пузырьки воздуха будут выходить при меньшем давлении. Пороговое давление назвали bubbles number (пузырьковое число). Для его определения поршень шприца устанавливают исходно на отметке 10 мл и замечают его положение в момент появления пузырьков. Эта величина в кубических сантиметрах и есть bubbles number. Оно равно числу 10, деленному на пороговое давление в атмосферах. Хотя пузырьковое число является лишь оценочным параметром и зависит от геометрии кончика, этот способ измерения размеров кончика более точный, чем метод, основанный на определении сопротивления, и позволяет оценивать размеры до заполнения электродов электролитом. По примерным оценкам, электроды с bubbles number 3-3,5 приемлемы для большинства типов регистрации, с 4-4,5 – для регистрации на целой клетке и с 1,5-2,5 – при работе с такими малыми, легко деформирующимися клетками, как эритроциты.
Для того чтобы получить те или иные конфигурации, необходимо прежде всего создать конфигурацию cell-attached. После подсоединения пипетки к держателю при помощи шприца подают небольшое положительное давление (примерно 0,01 мл) и вводят patch-пипетку в перфузионную камеру. При этом включается программа, которая создает прямоугольные импульсы электрического тока отрицательной полярности амплитудой не более -7 мВ и частотой 1 Гц при усилении х2. Подведя patch-пипетку к клетке, снимают давление в пипетке и касаются мембраны клетки. При работе с некоторыми клетками, например, с изолированными с помощью ферментов клетками миокарда или клетками скелетных мышц, гигаомные контакты иногда формируются спонтанно. При прикосновении кончиком пипетки к поверхности клетки высокоомный контакт образуется без подсасывания и даже при небольшом избыточном давлении в пипетке. Если спонтанного формирования гигаомного контакта не происходит, то в шприце на 1 мл, который соединен с patch-пипеткой, создают небольшое отрицательное давление (примерно 0,2 мл), в результате чего регистрируется повышение переходного сопротивления «стекло кончика patch-пипетки – мембрана клетки». Обычно в течение 1-1,5 мин это сопротивление достигает требуемых величин, например, 2-2,5 ГОм для кардиомиоцитов. Если этого не происходит и сопротивление прекращает увеличиваться при величине в диапазоне 500-700 МОм, то шприц можно снять, и во многих случаях увеличение сопротивления происходит за считаные секунды. Чем больше величина переходного сопротивления, тем более точно будет осуществляться последующая регистрация тока в той или иной конфигурации. После достижения величины переходного сопротивления 200 МОм включают программу, обеспечивающую генерацию импульсов электрического тока с необходимыми для эксперимента параметрами. Переключают усиление усилителя на х10 (или х20 при необходимости). Помимо регистрируемой величины переходного сопротивления можно ориентироваться в первом приближении на идущий одновременно с повышением сопротивления процесс уменьшения амплитуды прямоугольного импульса электрического тока. При указанном усилении о достижении необходимого переходного сопротивления свидетельствует отсутствие прямоугольного сигнала на экране монитора и наличие емкостных пиков, соответствующих фронту нарастания сигнала (в положительную область) и фронту падения сигнала (в отрицательную область).
Отдельный вопрос связан с раствором, которым заполняют patchпипетки. В стандартных микроэлектродных исследованиях для заполнения микроэлектродов обычно используют 2,5 М раствор KCl. Для patch-пипетки нужен тот раствор, состав которого определяется конкретными задачами экспериментатора.
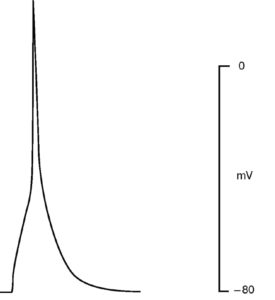
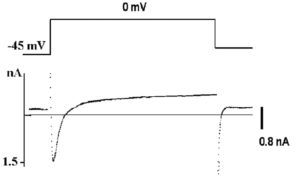
Рассмотрим этот вопрос, например, для patch-пипетки, которая будет использована для создания конфигурации whole-cell у изолированных кардиомиоцитов. Раствор для такой пипетки будет иметь прямую связь с внутриклеточным раствором, причем степень диффузии ионов и каких-либо соединений в клетку будет достаточно высока из-за низкого сопротивления (т.е. большого отверстия) patchпипетки. Некий «средний» внутриклеточный раствор кардиомиоцита включает: 15 мМ Na+, 145 мМ K+, 10-4 мМ Ca2+ и другие ионы, которые обычно не учитываются. Данные внутриклеточные концентрации ионов рассчитаны по свободным концентрациям в цитоплазме. С учетом известных внеклеточных концентраций ионов перфузионный раствор должен содержать 150 мМ NaCl, 5,4 мМ KCl, 1,8 мМ CaCl2, 1,2 мМ MgCl2, 20 мМ глюкозы и 5 мМ HEPES/NaOH (HEPES – N-2-hydroxyethylpiperazine-N’-2-ethanesulfonic acid) [pH=7,4]. В то же время раствор для patch-пипеток должен отвечать определенным требованиям, которые определяются тем, что исследователь хочет зарегистрировать. Поставим следующую задачу эксперимента. Нам необходимо зарегистрировать в режиме voltage-clamp суммарный ионный ток, включающий кальциевую и калиевую компоненты (рис. 4), и в относительно поддерживаемого потенциала величиной -45 мВ. Na+ подавлен поддерживаемым на уровне -45 мВ потенциалом. Перфузионный раствор содержит стандартный набор ионов: 150 мМ NaCl, 5,4 мМ KCl, 1,8 мМ CaCl2, 1,2 мМ MgCl2, 20 мМ глюкозы и 5 мМ HEPES/NaOH (pH=7,4). Раствор, заполняющий patch-пипетки, содержит 140 мМ KCl, 5,5 мМ MgCl2, 5 мМ Na2ATP, 0,01 мМ EGTA, 10 мМ HEPES/KOH (pH=7,2) режиме current-clamp зарегистрировать ПД кардиомиоцита (рис. 5). Для этих целей используют упомянутый выше перфузионный раствор, а раствор patch-пипетки должен соответствовать внутриклеточному раствору и включать в себя приблизительно 140 мМ KCl, 5,5 мМ MgCl2, 5 мМ Na2ATP, 0,01 мМ EGTA, 10 мМ HEPES/KOH (pH=7,2).
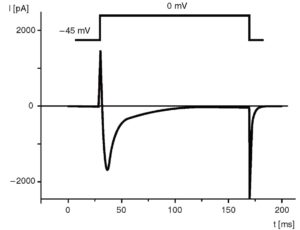
Если задача эксперимента включает в себя регистрацию только пика кальциевого тока, раствор должен включать в себя 140 мМ CsCl, 5,5 мМ MgCl2, 5 мМ Na2ATP, 0,01 мМ EGTA, 10 мМ HEPES/KOH (pH=7,2). В этом случае Cs+ выступает как блокатор калиевого тока. Для полного ингибирования Na+-TOKa можно добавить необходимое количество блокаторов Na+-каналов, имеющихся в данном типе клеток, хотя обычно правильно подобранная величина holding potential ингибирует Na+-ток. Разумеется, что во внеклеточном растворе 5,4 мМ KCl необходимо также заменить на 5,4 мМ CsCl (рис. 6).
Если же в дополнение к регистрации пика кальциевого тока необходимо изучать его инактивацию, экспериментатору следует ввести в пипетку соответствующие блокаторы калиевых каналов, поскольку присутствие только ионов Cs+ не даст необходимого эффекта блокирования всех каналов выходящего тока. Если при этом требуется следить за внутриклеточным Ca2+, то необходимо, чтобы в patchпипетке было фиксированное рСа. Так, при необходимости иметь pCa=6 patch-пипетки должны содержать 4,5 мМ CaCl2 и 5 мМ EGTA. При необходимости иметь pCa=7 patch-пипетки должны содержать 5 μM EGTA. Для создания pCa=8 patch-пипетки должны содержать 5 мМ BAPTA.
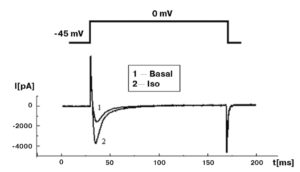
В заключение следует отметить, что добавление в patch-пипетку 5 мМ Na2ATP для предотвращения run-down каналов, на наш взгляд, не является необходимым. При хорошем выделении клеток они могут «висеть» в конфигурации whole-cell и без Na2ATP в patch-пипетке до 50 мин без каких-либо изменений своей электрофизиологии. Если же клетки «плохие», их электрофизиологические параметры (например, пиковый Ca2+-ток) линейно меняются (уменьшение пикового Ca2+-тока) в течение 10-15 мин, и это является обычной гибелью плохо сваренных клеток, а экспериментатор не может оправдывать ситуацию наступлением run-down, тем более что в этом случае присутствие Na2ATP совершенно не улучшает ситуацию. Читатель, планирующий работать с кардиомиоцитами, может для себя отметить, что, по нашему мнению, лучший тест качества клеток – введение в перфузионный раствор 10-30 нМ изопротеренола. На этом фоне у «хороших» клеток наблюдают увеличение Ca2+-тока L-типа не менее чем в 3 раза (рис. 7).
Принципы измерений тока в конфигурации whole-cell
После получения конфигурации cell-attached осуществляют компенсацию емкости, устраняя при помощи регулировки емкостные пики. После этого при помощи шприца резко создают отрицательное давление в patch-пипетке, перемещая поршень на 0,3-0,4 мл и тут же снимая шприц. Если разрыва мембраны не происходит, повторяют процедуру до получения конфигурации whole-cell.
Используемый для измерения токов алгоритм программы включает в себя следующие аспекты. Прежде всего, holding potential, или поддерживаемый потенциал, устанавливают, исходя из того, какой ток экспериментатор собирается регистрировать. Так, для изучения Na+-токов величина holding potential должна лежать в тех пределах, когда Na+-каналы практически не активированы и/или инактивированы; например, для кардиомиоцитов, потенциал покоя которых равен -80 мВ, holding potential должен быть несколько больше, например -85 мВ. При этом должны быть заблокированы Ca2+– K+-каналы (необходимо отметить, что заблокировать все K+-каналы достаточно сложно). При изучении Ca2+-токов величина holding potential должна составлять около -45 мВ, т.е. находиться на том уровне, когда инактивированы Na+-каналы, а Ca2+-каналы практически не активированы и/или инактивированы. При этом должны быть заблокированы K+-каналы и желательно (хотя и необязательно) Na+-каналы. Амплитуду тестирующего прямоугольного импульса электрического тока выбирают на основе известных вольт-амперных характеристик для данного типа каналов. Например, для L-типа Ca2+-каналов характерна максимальная величина тока при амплитуде тестирующего сигнала от -45 до 0 мВ. Что касается длительности тестирующего сигнала, то обычно исходят из задач эксперимента. Если необходимо измерять только величину тока по пику, например Ca2+-тока, то длительность прямоугольного импульса электрического тока должна лежать в пределах 140-150 мс. Если же необходимо оценить активацию и инактивацию Ca2+-тока, то длительность должна быть значительно большей. Длительность импульса зависит от задачи эксперимента, так же как и внутриклеточный раствор.
Общее правило: тестирующий импульс должен быть значительно больше длительности исследуемого процесса. Другими словами, если исследователя интересует время активации, то проводят серию экспериментов, используя разную длительность, определяют время активации и дальнейшие опыты производят, используя импульсы, скажем, в 3 раза длиннее (обычно применяют импульсы длиннее именно в 3 раза). Частота подачи сигнала определяется как задачами эксперимента, так и длительностью тестирующего импульса и параметрами (временем) выхода из инактивации.
Далее в программу должна быть включена возможность измерения вольт-амперной характеристики клетки. Для этого с шагом 10 мВ, а при приближении к точке пересечения оси абсцисс с осью ординат (т.е. к нулевой точке потенциала и тока) – с шагом 5 мВ от величины holding potential, должны быть поданы тестирующие импульсы отрицательной полярности до -100 мВ, после чего подают тестирующие импульсы положительной полярности до величины +100 мВ.
Наконец, должна быть предусмотрена программа для определения емкости клетки. Для этого от уровня -80 мВ (или несколько большего) на клетку подают тестирующий импульс отрицательной полярности величиной не более 10 мВ (на самом деле точная величина тестирующего импульса не так важна, хотя обычно на клетку подают действительно 10 мВ; важно, чтобы не активировался ни один ток) и регистрируют площадь емкостных пиков, соответствующих фронту нарастания сигнала (в положительную область) и фронту падения сигнала (в отрицательную область), вычисляя на этой основе емкость клетки. В этом случае используют простой расчет, связанный с RC-цепочкой. Если подать достаточно длинный импульс, то площадь под емкостным артефактом равна RC при соблюдении двух приближений. Необходимо: пренебречь фронтом нарастания; считать спад как моноэкспоненциальный.
Если импульс длинный, то ток в конце импульса дает величину R=U/I и, соответственно, можно подсчитать С. Емкость клетки необходима для нормирования величины тока, т.е. для получения значений pA/pF. Такое нормирование крайне важно, поскольку величина тока зависит от размеров клетки, определение которых практически невозможно. Другими словами, у разных по размеру клеток будут регистрироваться разные по величине токи, поэтому проведение статистического анализа очень сложно осуществить. Однако, поскольку размеры клетки напрямую связаны с ее емкостью, принято осуществлять нормирование по величине емкости.
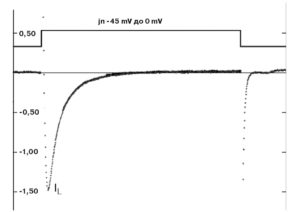
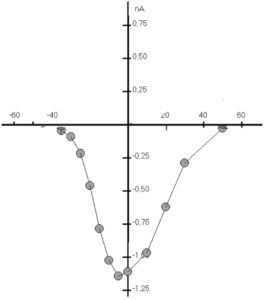
Типичный пример Са2+-тока рабочего кардиомиоцита, зарегистрированного методом patch-clamp в конфигурации whole-cell, представлен на рис. 8, а вольт-амперная характеристика клетки представлена на рис. 9. Для ее получения у вентрикулярных кардиомиоцитов мыши фиксировали потенциал на уровне -45 мВ и проводили его смещение импульсным током длительностью 140 мс до 0 мВ (красная кривая). На уровне фиксированного потенциала -45 мВ регистрировали отсутствие тока через мембрану клетки (рис. 8). При смещении мембранного потенциала до 0 мВ регистрировали входящий ICa-L-ток – ток через L-тип Ca2+-каналов и далее – поздние токи IL (ток). После окончания импульса электрического тока вновь регистрировали полное отсутствие тока через мембрану. Вольтамперную характеристику клетки (рис. 9) регистрировали при ступенчатом смещении мембранного потенциала тестируемыми импульсами от – 60 до +60 мВ относительно поддерживаемого потенциала, равного -45 мВ.
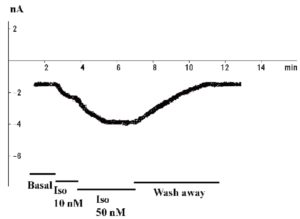
Еще один способ оценки величины изменения тока от времени – регистрация так называемого time course (рис. 10). Этим методом обработки данных по рисунку можно определить динамику изменения пикового тока, в данном случае Ca2+-тока L-типа – во времени, а также оценить влияние тех или иных соединений на величину тока. На рис. 10 показан базальный Ca2+-ток L-типа, который не меняется до введения изопротеренола в концентрациях 10 и 50 нМ, что приводит к его выраженной стимуляции. Кроме того, продемонстрирован эффект отмыва клетки от изопротеренола и возвращение тока к исходным значениям.
Еще два параметра, характеризующие работу потенциалуправляемых каналов, – их активация и инактивация. Активация потенциалуправляемых каналов, которая происходит только под влиянием изменения трансмембранного электрического потенциала, является их характерной чертой. Особенность Ca2+-токов по сравнению с Na+-токами заключается в их медленном нарастании при смещении мембранного потенциала. Этот процесс описывают моноэкспоненциальной функцией с постоянной времени активации (τa [ms]). Инактивация представляет собой процесс постепенного ослабления ионного тока через канал при продолжающейся деполяризации. Проявлением инактивации является спад вызванного деполяризующей ступенькой тока после достижения им пикового значения. Этот процесс имеет, как правило, сложную кинетику и обычно описывается двумя экспонентами:
Y = Y0 + A1e [ – (x-x0) / τfast ] + A2e [ – (x-x0) / τslow ] (1)
На основании этого уравнения определяют постоянные времени быстрой и медленной инактивации: и τslow . В уравнении Y0 [pA] отражает сдвиг нулевой линии (утечки) и в идеальном случае равен 0. X0 [ms] – время приложения деполяризирующего стимула. A1 [pA] – часть амплитуды тока, инактивирующаяся путем быстрой инактивации τfast , A2 [pA] – часть амплитуды тока, инактивирующаяся путем медленной инактивации τslow.Необходимо отметить, что максимальная амплитуда тока (Imax) есть сумма А1+А2. Поскольку максимальная амплитуда зависит от многих параметров, в частности типа, клетки, плотности Са2+-каналов и т.д., А1 и А2 часто нормализируют на максимальное значение тока (А/Imax и А2/Imax) и выражают в процентах (рис. 11, 12).
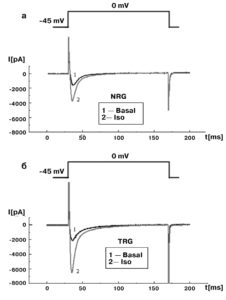
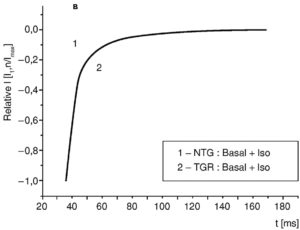
Рассмотрим эти вопросы подробнее. На рис. 11, а показан базальный ток (1) и его активация и инактивация под действием изопротеренола (2) у изолированных вентрикулярных кардиомиоцитов контрольных крыс. На рис. 11, б также показан базальный ток (1) и его активация и инактивация под действием изопротеренола (2), но у изолированных вентрикулярных кардиомиоцитов трансгенных крыс (SERCA2 overexpressing cardiomyocytes). В таких случаях обычно анализируют фазу инактивации Ca2+-тока.
Таблица 1. Типичное представление данных по инактивации тока
| 0 | 0 | Y0 | X0 [pA] | A1, % | τf [ms] | A2, % | τS [ms] |
|---|---|---|---|---|---|---|---|
| WT | Basal | 0 | -1557 | 82+0,6 | 9,80+0,61 | 18+0,6 | 64,04+1,52 |
| Iso | 0 | -3692 | 80+0,5 | 8,94+0,54 | 20+0,5 | 60,33+2,23 | |
| TR | Basal | 0 | -1937 | 65+0,4 | 8,45+0,83 | 35+0,4 | 74,32+1,10 |
| Iso | 0 | -6432 | 79+0,6 | 7,39+0,76 | 21+0,6 | 61,34+2,45 |
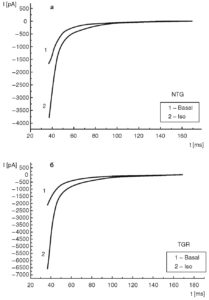
Выведем отдельно фазы инактивации Ca2+-тока, пока еще не нормируя данные на рис. 12, а для контрольных животных и на рис. 12, б – для трансгенных, и представим в соответствии с вышеописанным принципом часть данных Y0, X0 [pA], A1 (%), A2 (%) в форме табл. .1. Далее А1 и А2 нормализируем на максимальное значение тока( A1/Imax и A2/Imax) и проведем расчет данных τf [ms] и τs [ms], которые представим в таблице. Таким образом, табл. 1 будет иметь законченный вид, а совмещение нормализованных кривых инактивации, представленное на рис.12, в с учетом величины стандартной девиации, продемонстрирует нам, что β-адренергическая стимуляция клеток контрольных и трансгенных животных полностью устраняет исходную разницу в инактивационной кинетике.
Корректное описание инактивации Ca2+-токов представляет определенные сложности, поскольку этот процесс развивается во времени параллельно с развитием выходящих К+-токов. Именно поэтому регистрируемый спад Са2+-тока может быть не истинным, а определяться наложением на Са2+-ток одновременно развивающихся выходящих К+-токов. Для предотвращения подобных ошибок необходимо тщательно блокировать К+-токи. Их наличие в наиболее простой форме можно определить по амплитуде Са2+-тока в конце достаточно длинного по времени стимула. В этом случае она будет слегка превышать нулевую линию (Y0 >0). Здесь следует отметить, что превышение нулевой линии в конце стимула может также отражать очень медленную (константа времени значительно больше длительности стимула) инактивацию исследуемого Са2+-тока, поэтому, чтобы избежать возможных ошибок, сложный динамический процесс инактивации сводят к стационарной (steady-state) инактивации.
При этом измеряют уменьшение максимальной величины тока, вызванного тестирующими деполяризующими ступеньками в случае, если перед этим мембранный потенциал определенное (достаточно длинное по сравнению с длительностью инактивации) время поддерживался на сниженном уровне. Зависимость этого уменьшения от величины поддерживаемого потенциала носит S-образную форму. Тогда для характеристики Са2+-каналов помимо амплитуды кальциевого тока (ICa) обычно рассматривают величину активации (Va) и величину инактивации (Vh). Если сущность постоянных времени активации и инактивации Са2+-каналов достаточно понятна, то величины активации (Va) и инактивации (Vh) требуют пояснения.
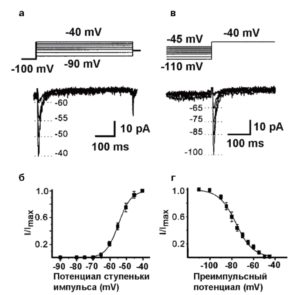
На рис. 13 показаны принципы исследования активации и инактивации на примере IT Са2+-тока. На панели А (см. рис.13) представлены тестовые сигналы и steady-state активация IT. Мембрана клетки находилась на поддерживаемом потенциале – 100 мВ – в течение 1 с, и Са2+-токи определяли при помощи деполяризующих шагов-cтупенек. На панели Б (см. рис. 13) показана активационная кривая, полученная на основании уравнения Больцмана в следующей форме:
I/Imax = 1 / [ 1 + exp (- ( V – V0.5)/k]
где I представляет собой амплитуду тока, Imax является максимальной амплитудой тока, V – тестовый потенциал, V0,5 – потенциал полуактивации, или, иначе Va.
На панели В (см. рис.13) представлены тестовые сигналы и steady-state инактивация IT,Ca. Мембрана клетки находилась на поддерживаемом потенциале в диапазоне от -110 до -45 мВ в течение 1 с, и Са2+-токи определяли при помощи деполяризующих шаговступенек до -40 мВ. На панели Г (см. рис. 13) показана инактивационная кривая, полученная на основании уравнения Больцмана в следующей форме:
I/Imax = 1 / [ 1 + exp ( ( V – V0.5)/k] (3)
где I представляет собой амплитуду тока, Imax является максимальной амплитудой тока, V – тестовый потенциал, V0,5 – потенциал полуинактивации или иначе Vh.
И в случае Б, и в случае Г константа k представляет собой наклон кривой (фактор крутизны) и отражает steady-state потенциал – чувствительность каналов, или диапазон потенциалов, в котором каналы функциональны. Чем больше k, тем уже диапазон.
Принципы измерений тока, протекающего через одиночные каналы
В какой бы конфигурации канальные токи мы не регистрировали, прежде всего необходимо рассмотреть вопрос о величине фрагмента мембраны, который находится под patch-пипеткой. Это особенно важно при изучении реагирующих на изменение давления механосенситивных каналов.
Итак, после спонтанного получения гигаомного контакта без подсасывания при визуальном рассмотрении кончика patchпипетки и поверхности клеточной мембраны при большом увеличении (х1200) не наблюдается деформации клеточной мембраны под patch-пипеткой. Площадь электрически изолированного пипеткой мембранного фрагмента, по-видимому, примерно равна площади отверстия кончика. Область контакта «мембрана-стекло» формируется, вероятно, только торцом кончика patch-пипетки. В этом случае площадь фрагмента мембраны можно оценить по значению сопротивления patch-пипетки до образования контакта. Однако в большинстве случаев контакт формируется только при небольшом отрицательном давлении, создаваемом внутри пипетки. При этом часть клеточной мембраны втягивается внутрь кончика пипетки, принимая Q-образную форму. Такую деформацию во время установления гигаомного контакта можно наблюдать даже в световой микроскоп и затем оценивать площадь мембранного фрагмента в кончике patch-пипетки. Подробно этот вопрос будет обсужден в главе, посвященной механосенситивным ионным каналам.
Можно примерно оценивать площадь втянутых в кончик patchпипетки участков мембраны в двух экспериментальных ситуациях. В первом случае мембранный фрагмент втягивают в кончик пипетки до тех пор, пока не образовывается гигаомный контакт. Степень деформации мембраны можно оценить при увеличении х500 или х1250, используя или водно-иммерсионный объектив (х40) в обычном микроскопе, или объектив с масляной иммерсией (х100) в инвертированном микроскопе. При получении боковой проекции пипетку располагают так, чтобы ее ось была почти параллельна (отклонение <10°) фокальной плоскости. Мембранный фрагмент изолируют механически от остальной части мембраны отведением кончика пипетки на расстояние 20-50 мкм от поверхности клетки и на этом этапе фотографируют кончик пипетки. При создании дополнительного отрицательного давления patch-пипетки фрагмент перестает контактировать со стеклянной стенкой и принимает форму сферического пузырька (везикулы), который перемещается в кончике вверх и вниз. Прикладывая небольшое положительное давление (<5 см Н2О), пузырек вводят в самый кончик пипетки и фотографируют. С помощью таких микрофотографий определяют площадь мембранных фрагментов, втянутых в кончик пипетки при образовании гигаомного контакта. Таким образом, при стандартном сопротивлении patch-пипетки можно оценить площадь фрагмента в Ω-образной конфигурации (т.е. когда мембранный фрагмент находится в контакте со стенкой пипетки) и после образования везикулы.
Площадь мембраны в Ω-образной конфигурации можно оценить, если представить фрагмент в виде конуса, имеющего определенную площадь взаимодействия со стеклом, и полусферу, обращенную к раствору в patch-пипетке. В везикулярной конфигурации площадь фрагмента оценивают по величине его кажущегося диаметра.
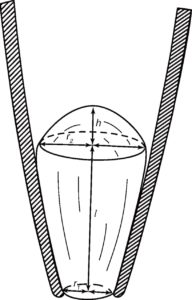
В Ω-образной конфигурации отношение площади полусферы к площади мембраны, контактирующей со стеклом, составляло 0,5-0,6. Значения общей площади мембраны в двух конфигурациях – Ω-образной и везикулярной – почти одинаковы. Поскольку площадь везикулы можно оценить точнее, измерения лучше выполнять в этой конфигурации. Средняя площадь мембранных фрагментов, изолированных пипетками с сопротивлением 2,5 МОм и исследованных в везикулярной конфигурации, составляет в среднем 14 мкм2. Предполагая, что эти фрагменты имеют геометрическую форму, изображенную на рис. 14 (т.е. отношение площади полусферы к площади мембраны, контактирующей со стеклом части, составляет 0,5), получим площадь полусферы мембраны порядка 5 мкм2.
Теперь перейдем непосредственно к принципам регистрации одиночных ионных каналов, которую осуществляют в режиме voltage-clamp. Уже создав конфигурацию cell-attached или конфигурации inside-out patch и outside-out patch, при достаточно высоком значении cell-attached и величине усиления усилителя можно зарегистрировать одиночные ионные каналы, расположенные под пипеткой. Основной принцип регистрации того или иного типа одиночного ионного канала заключается в том, что экспериментатор должен иметь информацию о величине поддерживаемого потенциала для этого типа канала и об амплитуде тестируемого потенциала относительно поддерживаемого потенциала, при которой этот канал активируется. Рассмотрим ряд примеров регистрации некоторых одиночных Ca2+-каналов.

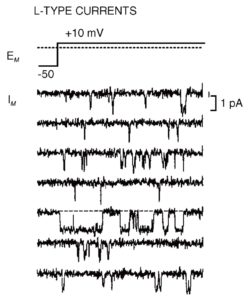
На рис. 15 продемонстрированы одиночные Са2+-каналы Т-типа, а на рис. 16 – одиночные Са2+-каналы L-типа. В обоих случаях открытое состояние Са2+-каналов представлено в виде смещения нулевой линии вниз, т.е. через канал течет входящий ток.
Хотя ток, текущий через каналы, регистрируется и представлен в амперах (пА, нА), обычно после обработки обсуждают проводимость одиночных каналов и используют в качестве единиц измерения сименсы (пС, нС). Это связано с тем, что амплитуда тока определяется не как электрическая, а как электрохимическая разность потенциалов: I[pA]=(Um-Urev)/R. Поскольку после изобретения метода диализа клеток появилась возможность менять как потенциал, так и среду внутри и снаружи клетки, то измеренный ток отражает как изменение потенциала на мембране Um, так и потенциала реверсии Urev. Чтобы не заставлять читателя следить за потенциалом реверсии: смотреть растворы и постоянно помнить, какие ионы и в каких количествах находятся снаружи и внутри, применили понятие «проводимость»; таким образом, экспериментатор сам должен посчитать электрохимическую разность потенциалов и поделить на нее измеренный ток. Это имеет смысл для каналов с линейной вольтамперной характеристикой, поскольку дает параметр, не зависящий от условий эксперимента. Для «сложных» потенциалозависимых каналов (например, кальциевых) все равно пишут дополнительно и потенциал, и состав раствора.
Таким образом, принципиально регистрация одиночных каналов не вызывает каких-либо затруднений (при условии наличия современной аппаратуры и хорошо приготовленных клеток). Главный вопрос заключается в том, по каким правилам и как обработать огромный объем информации, регистрируемый от канала. Без хорошего программного обеспечения решить эту проблему практически невозможно. Что же экспериментатор ждет от анализа получаемой информации? Прежде всего, это наличие качественных изображений зарегистрированной канальной активности, что определяется хорошим техническим обеспечением и хорошим персональным компьютером (гигагерцевого диапазона) с современной программой обработки. Более сложный вопрос – принципы самой обработки множества данных и их интерпретация. Для глубокого понимания этой задачи необходимо свободно ориентироваться в теории вероятностей и статистическом анализе – в тех областях знаний, которые в подавляющем большинстве отсутствуют у ряда экспериментаторов.
В основе механизмов, которые исследуют при описании работы ионных каналов, лежат обратимые переходы между различными дискретными состояниями, в которых могут находиться каналы.
Для потенциалуправляемых каналов этот механизм в самом простом случае можно проиллюстрировать следующим выражением:
Рядом со стрелкой, изображающей данный переход, ставят константу скорости перехода. В приведенном случае существуют только 2 состояния канала.
Если речь идет о лигандуправляемых каналах, то для их активации необходимо связывание лиганда и рецептора, поэтому у канала будет 3 дискретных состояния:
В этом случае канал имеет 2 закрытых дискретных состояния и 1 открытое. Поскольку patch-пипеткой, связанной с соответствующей аппаратурой, мы измеряем какую-либо характеристику большого числа регистрируемых каналов, то можно оценивать эту характеристику только как среднюю величину. Например, если скорости перехода между открытым и закрытым состоянием канала постоянны (не изменяются во времени), то временной ход среднего тока I(t) через ионные каналы будет описываться Σ(k-1) экспонент, где k – число состояний системы.
Известно, что скорость любой реакции на основании закона действующих масс пропорциональна произведению концентраций реагентов. Константу пропорциональности называют константой скорости, причем полагают, что она не изменяется во времени, т.е. является истинной константой (α, β , k+1, k1). Однако применительно к ионным каналам существует несколько ограничений.
Так, константа скорости закрытия канала α зависит от величины мембранного потенциала, поэтому она будет истинной константой только в случае постоянного мембранного потенциала, а именно – при применении voltage-clamp. В обычной химической кинетике константа скорости описывает скорость реакции, например скорость закрытия канала (константа α), однако при рассмотрении одиночного канала необходимо учитывать, что это закрытие происходит случайным образом, поэтому ту же константу а следует рассматривать с позиций вероятностных соображений. Другими словами, а есть мера вероятности того, что открытый канал закроется в течение единицы времени. Однако константа α имеет размерность [с-1] и, следовательно, это не просто безразмерная вероятность.
Прежде всего, нас будет интересовать тот отрезок времени, в течение которого канал будет находиться в том или ином состоянии. Эти отрезки времени являются случайными переменными, и характер их вариации описывается вероятностным распределением. Время представляет собой непрерывную переменную, поэтому необходимо искать функцию плотности вероятности, например для времени жизни канала в открытом или закрытом состоянии. Эта функция f(t) определяется таким образом, что площадь под кривой, рассчитанная до момента времени t, представляет собой вероятность того, что время жизни, например в открытом состоянии, меньше или равно t. Существует ряд способов, позволяющих найти вид этого распределения, но на данных вопросах мы останавливаться не будем, предоставляя читателю возможность обратиться к специализированной литературе. Для наиболее простого механизма, определяемого уравнением:
Времена жизни в открытом состоянии распределены экспоненциально со средним временем, равным 1/α, а для времен нахождения в закрытом состоянии справедливо нижеприведенное выражение:
f(t)=β’ x e-β’t (2.4)
Таким образом, эти времена распределены экспоненциально со средним значением 1/β’ для одиночного канала.
Тот факт, что временной ход среднего тока через большое число ионных каналов и распределение времени жизни элементарных событий подчиняются экспоненциальному закону, не является случайным. Наиболее простая ситуация, которую обычно рассматривают для пояснения, представляет собой пример с ионотропным каналом и медиатором в виде ацетилхолина. Пусть в момент времени 0 под действием кванта медиатора ацетилхолина синхронно откроется какое-то число ионных каналов. После этого ацетилхолин исчезнет, в связи с чем канал, закрывшись, не имеет никакой возможности открыться вновь. Длительность интервалов времени, в течение которых каждый канал остается открытым, подчиняется экспоненциальному распределению (рис. 17, а), а следовательно, интегральный ток через большое число таких каналов тоже будет падать экпоненциально (рис.17, б).
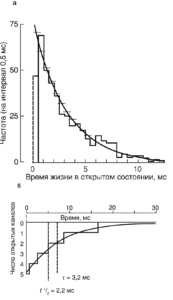

Важный момент – построение гистограмм и функций плотности вероятности. При анализе активности одиночных каналов, как правило, приходится иметь дело с непрерывными переменными (время нахождения в открытом состоянии и т.д.), а не с дискретными или целочисленными. Распределение вероятности непрерывной переменной можно задать функцией плотности вероятности. Эта функция определяется так, что площадь под ее графиком представляет собой вероятность (или частоту). Чаще всего функция плотности вероятности является экспонентой или суммой экспонент. Например, если временной интервал имеет простое экспоненциальное распределение со средним τ=1/λ , то его функция плотности вероятности выглядит как
f(t)=λ’ x e-λхt , t>0.
В практическом применении эти данные представлены идеализированной записью времен переходов, или временных интервалов. Данную запись можно просматривать, чтобы убедиться, что временное разрешение достаточно. Из идеализированной записи можно извлечь все, что для нас представляет интерес: времена жизни открытого состояния, закрытого состояния и др. Данные могут включать серию из n времен жизни в открытом состоянии: t1, t2 … tn. Допустим, что они равны, например, 1,41; 5,82; 3,91; 10,9 … 6,43 мс. Функция плотности вероятности в первом приближении пропорциональна вероятности того, что наблюдаемое время жизни попадет внутрь интервала от t до t + Δt, где Δt – бесконечно малая величина.
Однако мы не можем работать с бесконечно малыми интервалами и, следовательно, представлять данные в виде функций плотности вероятности, но мы можем воспроизвести некоторую аппроксимацию функций плотности вероятности путем подсчета числа наблюдений, попадающих в интервалы (бины) определенной ширины. Для представленного выше примера в качестве ширины бина можно взять 1 мс и подсчитать число наблюдений, приходящихся на интервалы между 0 и 1 мс, 1 и 2 мс и т.д. Затем можно представить данные в форме гистограммы, как показано на рис. 2.18. Такая гистограмма является разрывной (дискретной), и ее ординаты представляют собой безразмерные числа. С другой стороны, функция плотности вероятности, для которой гистограмма служит неким приближением, непрерывна и имеет размерность [с-1].
Для представления коротких интервалов лучше пользоваться бинами малой ширины, а для длинных интервалов – бинами большей ширины (обычно коротких интервалов больше, чем длинных, и функция плотности вероятности в области малых времен падает наиболее круто). Таким образом, если мы определяем ординату как, например (плотность частоты)/2 мс, то ордината бина шириной 2 мс (скажем, между 6 и 8 мс) соответствует действительному числу наблюдений, приходящихся на этот бин. Однако если более короткие интервалы представляются графически с шириной бина равной 1, а не 2 мс, то в этом случае ордината (высота бина) равна удвоенному числу действительных наблюдений, попадающих в бин от 1 до 2 мс (так, что площадь все равно соответствует общему числу наблюдений).
Интерпретация гистограммы распределения времен жизни в открытом состоянии обычно довольно сложна. Классически предполагается, что минимальное время жизни очень короткое (неразрешимое технически). Тогда экспонента – наиболее вероятная аппроксимирующая функция, и ее постоянная спада (т) дает среднее время жизни в открытом состоянии. В некоторых случаях распределение бывает явно не экспоненциальное, т.е. не максимальное возле нуля. В связи с этим обычно необходимо следить за тем, какую функцию взяли авторы и почему. Типичная ошибка, например, пачечное открытие канала, когда наблюдают длинное событие только потому,
В зарубежной литературе по одной из осей графика можно встретить «N events», т.е. число событий. Иногда используют также «N of bin events» – число событий в столбце.
В профессиональной литературе часто оговаривают (обычно с точки зрения сигнал/шум) и указывают ширину столбца (bin), поскольку от нее очень зависит распределение.
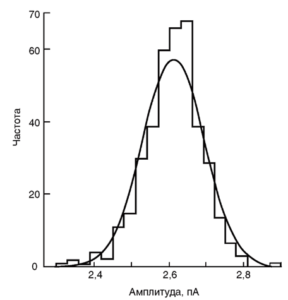
Амплитуды токов через одиночный канал в большинстве случаев хорошо согласуются друг с другом. Например, распределение амплитуд на рис. 19, аппроксимированное (условно) гауссовой кривой, дает среднее значение 2,61 пА со стандартным отклонением, равным 0,08 пА (т.е. 3,1% от среднего значения). Изменчивость в амплитуде от одного включения к другому для одного и того же канала или для разных каналов в мембранном фрагменте, по-видимому, очень мала. Она, вероятно, не превышает ошибки в «подгонке» амплитуды. Следовательно, в практическом смысле амплитуда по существу не является случайной переменной, как время пребывания в открытом состоянии, и представляет собой более или менее фиксированную величину.
В некоторых экспериментах на фрагментах мембраны наблюдают различия в амплитуде токов. Это может быть обусловлено работой двух разных независимых типов каналов, например, синаптических и внесинаптических ионных каналов, активируемых ацетилхолином. С другой стороны, это может быть следствием множественности подсостояний проводимости каналов одного и того же типа, которую наблюдали Hamill и Sakmann6. Данные такого рода приходится аппроксимировать суммой одного или более распределений Гаусса (или суммой других распределений), используя метод максимального правдоподобия. Эта процедура совершенно аналогична процедуре, применяемой для аппроксимации суммой экспоненциальных распределений.
Распределение амплитуд может служить индикатором множественности популяций каналов или подуровней проводимости. Если отдельные пики в амплитудном распределении достаточно хорошо различимы, то можно разграничить переходы на идеализированной записи в соответствии с разными амплитудами и затем анализировать серии событий с разной амплитудой по отдельности.
Обычно предполагают, что амплитудная гистограмма хорошо описывается кривой Гаусса, если под пипеткой находится один канал у него есть только одно открытое состояние – как показано на рисунке. Гауссовская аппроксимация дает среднюю амплитуду тока (событий) и погрешность аппроксимации (стандартное отклонение), т.е. лучше всегда писать, к примеру, 1,5±0,5 пА.
➥ Читайте также: Техника patch clamp на срезах мозга
Footnotes
- Костюк П.Г., Крышталь О.А. Механизмы электрической возбудимости нервной клетки. – М.: Наука, 1981. – 204 с.
- Магура И.С. Проблемы электрической возбудимости нейрональной мембраны. – Киев: Наукова Думка, 1981. – 206 с.
- Neher E, Sakmann B. Single-channel currents recorded from membraneof denervated frog muscle fibres // Nature. – 1976. – Vol. 260 (5554). – P. 799-802.
- Hamill O.P., Marty A., Neher E. et al. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches // Europ. J. Physiol. – 1981. – Vol. 391 (2). – P. 85-100.
- Hamill O.P., Sakmann B. Multiple conductance states of single acetylcho-line receptor channels in embryonic muscle cells // Nature. – 1981. -Vol. 294 (5840). – P. 462-464.
- Hamill O.P., Sakmann B. Multiple conductance states of single acetylcho-line receptor channels in embryonic muscle cells // Nature. – 1981. -Vol. 294 (5840). – P. 462-464.
