Метод независимых компонент

Метод независимых компонент (independent component analysis, ICA) – это метод анализа ЭЭГ, основанный на разделении многомерного сигнала на обособленные подкомпоненты (составляющие), которые независимы друг от друга. 

История 

Дженни Эро и Бернард Анс в 1984 году начали работу по созданию метода независимых компонент, а Христиан Джуттен продолжил работать над ICA. Наиболее полно метод описал Пьер Комон в 1994 году. Тони Белл и Терри Седжновски создали наиболее быстрый алгоритм infomax (ищет обособленные сигналы при помощи максимизации энтропии (меры неупорядоченности системы) через год после работы П. Комона. Некоторые авторы приравнивают этот принцип к методу максимального правдоподобия (поиск значения параметра генеральной совокупности, при котором имеющаяся выборка становится наиболее вероятной).1

Суть метода

ICA можно объяснить на примере коктейльной вечеринки (см. рис. 1). Представим, что в какой-нибудь комнате есть несколько микрофонов и несколько людей, которые разговаривают, поют, шумят. Задача – разделить пение, разговоры и шум. Для этого и применяется метод независимых компонент.

Метод помогает выделять IC (независимые компоненты, в данном случае “Hello” и “Namaste”) из смеси звуков, сигналов. После применения ICA получают разделенные сигналы. 

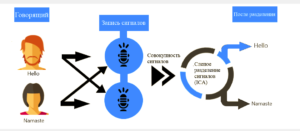
Рисунок 1. Принцип метода независимых компонент на примере коктейльной вечеринки

Объяснить механизм возможно следующим образом: представим, что наш датчик (например, микрофон или электрод) фиксирует некоторый сигнал, состоящий из нескольких наложенных друг на друга компонентов. В случае со звуком этими компонентами могут быть голоса собеседников, шум окружающего мира и музыка, как в примере с “коктейльной вечеринкой”, а в случае с ЭЭГ – моргание, движение глаз и собственно биоэлектрическая активность мозга. Все сигналы смешаны и взаимно искажают характеристики, накладываясь друг на друга.

Однако стоит заметить, что, несмотря на наложение, сигналы друг от друга независимы – это одно из ключевых положений метода независимых компонент. Соответственно, из совокупности полученных сигналов можно выделить необходимую составляющую. Для этого параметры сигнала (его амплитуда, частота, спектр) записываются в виде математических величин в специальную таблицу, элементы которой взаимосвязаны. Затем, с помощью ряда математических операций, из этой таблицы вычленяются элементы, относящиеся к тем или иным компонентам. Т.е. происходит разделение всей совокупности величин на группы, каждая из которых описывает тот или иной элемент итогового сигнала.

Таким образом, после разделения записанного сигнала мы получаем возможность удалить из него ненужные для нас элементы – шум голосов и музыку в примере с вечеринкой или моргание и другие помехи в случае ЭЭГ. Это позволяет нам очистить запись от лишних данных или же выделить конкретную информацию.

Математические принципы

Метод независимых компонент основан на том, что записанные n сигналов являются линейной комбинацией m неизвестных базовых сигналов.2 Математическая модель ICA в случае, если An*m – матрица с элементами n*m, а x – вектор строки, выглядит следующим образом. Ниже представлены формулы преобразованного базового сигнала.

x_{j}^{*}(k)=\sum_{i=1}^{n} a_{j i} s_{i}^{*}(k)+\varepsilon_{j}(k), K=1, \ldots, m

x^{*}(k)=A s^{*}(k)+\varepsilon(k), где s^{*}(k)=\left[s_{1}^{*}(k), s_{2}^{*}(k), \ldots, s_{n}^{*}(k)\right]^{T}  – независимый базовый сигнал, а \varepsilon(k)\left[\varepsilon_{1}(k), \varepsilon_{2}(k), \ldots, \varepsilon_{n}(k)\right]^{T} – аддитивный шум и Anxm – искомая матрица смешивания. Методы отыскания как матрицы An*m, так и вектора источников s*(k) могут быть различными и здесь не рассматриваются.

Этапы ICA

ICA базируется на двух принципах:

  1. сигналы обособлены;
  2. значения каждого сигнала имеют распределение, отличающееся от нормального;

Каждый из алгоритмов ICA (Infomax, FastICA, JADE, ядерный независимый компонентный анализ) включает в себя несколько обязательных частей:

  1. центрирование (вычитание среднего вектора и создание переменной с нулевым средним для упрощения проведения ICA)
  2. уменьшение размерности (использование PCA);
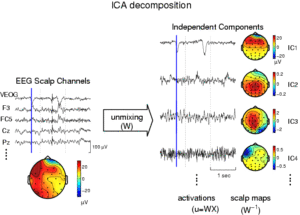
  3. декорреляцию (получение путем преобразований нового вектора, который является белым, то есть его компоненты не коррелируют друг с другом, и их дисперсии равны единице. Наиболее часто для этого применяется спектральное разложение матрицы)3 (см. рис. 2)
  4. очистка сигнала от артефактов (см. рис. 3)
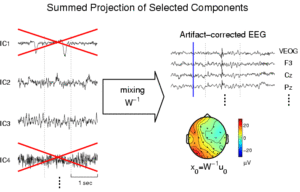
Рисунок 2. Этапы ICA. Пунктирная линия обозначает воздействие стимула. IC1, IC3, IC4 – артефакты. IC2 – компонент, отражающий активность головного мозга. Слева представлены необработанные данные ЭЭГ, которые подвергаются разложению на независимые компоненты. Справа также представлены проекции компонент на схематичное изображение головы
Рисунок 3. Этапы ICA. Последовательно показаны очистка сигнала от артефактов и его рекомпиляция

Алгоритмы ICA

1. FastICA

FastICA – один из наиболее используемых методов ICA, который основан на увеличении степени негауссовости (распределение, отличающееся от нормального распределения) и включает в себя алгоритм дефляции и симметричный алгоритм.4 Разница между этими двумя алгоритмами заключается в следующем: при дефляции сигналы извлекаются последовательно, один за другим (поэтому такой метод извлечения сигналов называют еще одноэлементным алгоритмом), а при симметричном извлечении оценка компонентов происходит параллельно в одно время. Принцип работы FastICA основан на использовании центральной предельной теоремы (утверждает, что при сложении довольно-таки большого количества слабо зависимых компонентов получается распределение данных, близкое к нормальному) и негэнтропии (мера упорядоченности системы). Он отличается от  Infomax быстротой применения.

2. Infomax

Этот метод базируется на минимизировании общей для компонентов информации при помощи максимизации энтропии. При сравнении алгоритма дефляции, симметричного алгоритма и Infomax выявлено, что наибольшей точностью обладает Infomax, затем симметричный алгоритм FastICA, а после – алгоритм дефляции.5

Иллюстрация работы метода

Пример работы метода независимых компонент представлен на рисунках 4-6.

Рисунок 4. ICA в магнитоэнцефалографии (МЭГ).[efn_note]R. Vigário, V. Jousmäki, М. Hämäläinen, R. Hari, E. Oja. Independent Component Analysis for Identification of Artifacts in Magnetoencephalographic Recordings. В кн.: Advances in Neural Information Processing Systems 10: материалы Neural Information Processing Systems (NIPS), 1997.[/efn_note] Первые два компонента (IC) являются результатом мышечной активности после воздействия механического раздражителя; IC3 – результат движения глаз по горизонтальной линии; IC4 компонент представляет сердечный артефакт; IC5 – выявляется как следствие моргания глаз; IC6 и IC7 – компоненты возникают в процессе дыхания; IC8 возникает в правой части магнитометра, а IC9 показывает наибольшее среднеквадратичное отклонение
Рисунок 5. A – исходные данные, запись ЭЭГ-сигнала. B – выделенные и удаленные впоследствии артефакты. C – скорректированная запись ЭЭГ-сигнала. D – сравнение скорректированных (пунктирные линии) и исходных данных.Рис. 5. A – исходные данные, запись ЭЭГ-сигнала. B – выделенные и удаленные впоследствии артефакты. C – скорректированная запись ЭЭГ-сигнала. D – сравнение скорректированных (пунктирные линии) и исходных данных
Рисунок 6. Выделение компонент и удаление артефактов с помощью ICA. Слева направо: необработанные данные ЭЭГ, выделенные независимые компоненты, проекция их на кожу головы и результат – скорректированный сигнал ЭЭГ

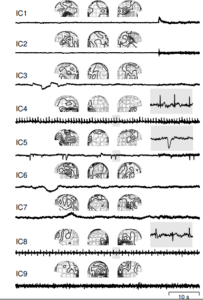
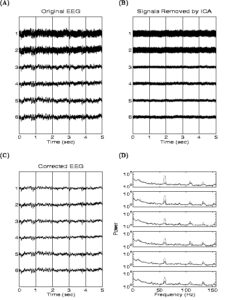
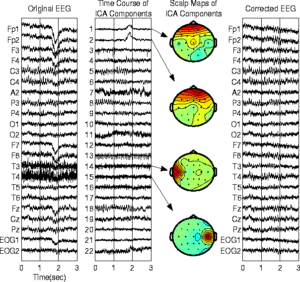
Преимущества перед методом главных компонент

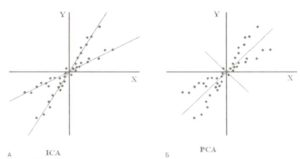
Целью ICA при анализе ЭЭГ является разделение многокомпонентного ЭЭГ-сигнала на части и удаление шумов и помех, вызванных морганием, движением глаз, сокращениями миокарда и мышечной активностью. По сравнению с методом главных компонент (principal component analysis, PCA) ICA является более эффективным методом удаления широкого ряда помех из записи ЭЭГ-сигнала, поскольку сохраняет больше информации об электрической активности мозга, лучше выделяет артефакты и отражает структуру распределения данных (см. рис. 25).

Рисунок 25. Сравнение PCA и ICA

Достоинства/недостатки

Преимуществами метода независимых компонент являются:

  1. условие ортогональности (независимости) компонент не является обязательным;
  2. нет необходимости в наличии канала для измерения параметров артефакта;
  3. возможность снизить нагрузку на оборудование, убрав ненужные каналы;
  4. возможность получать данные с точек с любым уровнем сигнала

К недостаткам метода относится:

  1. нельзя выделить источников больше, чем количество используемых электродов;
  2. необходим больший объем вычислений, чем, например, при регрессионном анализе.

Программное обеспечение

Программное обеспечение, которое позволяет удалять артефакты – WinEEG, EEGLAB (Matlab), WICA и AWICA.

WinEEG 

➥ Основная статья: WinEEG

В программе WinEEG существует три способа коррекции артефактов:

  1. удаление вручную – является трудоемким, почти полностью лишен объективности и ведет к разнообразным результатам и даже ошибкам в зависимости от опыта работы в данной программе.
  2. автоматическая разметка и удаление артефактов
  3. метод пространственной фильтрации – используется для удаления артефактов движения глазных яблок.

Программа WinEEG допускает работу с форматами файлов: .eeg, .erp, .spc, .erd. Для ручного удаления артефактов необходимо воспользоваться инструментом “Вырезать”, находящимся в меню “Правка”, предварительно выделив область предполагаемого артефакта. 

При автоматической разметке и коррекции фрагменты электроэнцефалограммы, которые соответствуют следующим критериям, рассматриваются как нежелательные:

  1. амплитуда сигнала выше 100 мкВ;
  2. амплитуда медленных волн в диапазоне частот от 0 до 1 Гц выше 50 мкВ;
  3. высокочастотная активность в диапазоне частот от 20 до 35 Гц выше 35 мкВ.

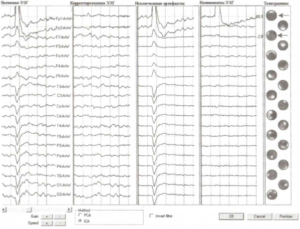
Алгоритм автоматического удаления артефактов в программе показан на рисунке 7, пространственная фильтрация изображена на рисунке 8. 

Рисунок 7. Удаление артефактов в программе WinEEG. Для автоматического удаления артефактов необходимо установить пороговые значения амплитуды сигналов (для медленных и высокочастотных волн в соответствии со значениями нежелательных компонентов, которые указаны выше) и нажать кнопку “Ok”. Программа отметит синим цветом артефакты, и они не будут учитываться
Рисунок 8. Удаление артефактов пространственной фильтрацией. В меню “Анализ” выбрать “Коррекцию артефактов”. Выбираем в качестве метода “ICA”, и справа получим топограммы ICA-компонент

MATLAB

➥ Основная статья: MATLAB

Рисунок 9. Начало работы. Выбрать “Set Path”
Рисунок 10. Интерфейс среды Matlab. Нажимаем Set Path, и выбираем папку с которой будем работать “Add with Subfolders”
Рисунок 11. Находим папку “eeglab…” и далее “Open”. После этого необходимо нажать на “Close” и в окне на рис. 11 выбрать “No”
Рисунок 12. Завершение выбора папки для работы
Рисунок 13. Для запуска программы EEGLAB в среде MatLAB необходимо в окне после “Trial” ввести “eeglab” и нажать ENTER

EEGLAB

➥ Основная статья: EEGLAB

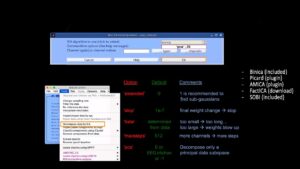
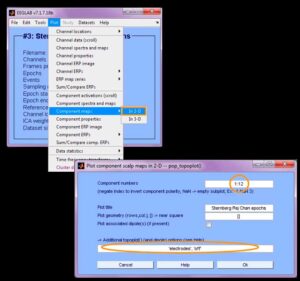
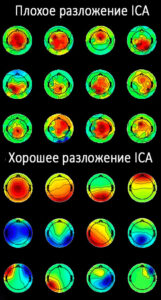
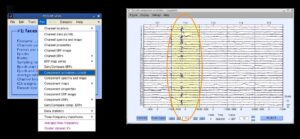
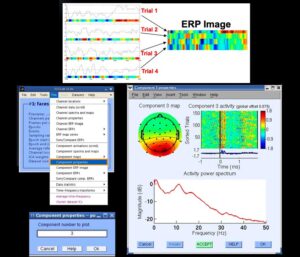
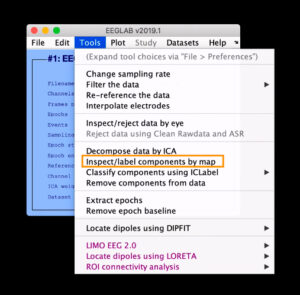
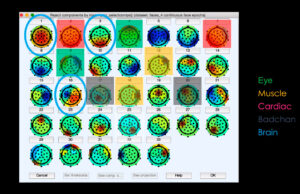
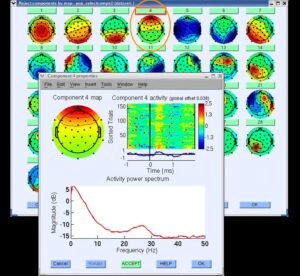
Для начала необходимо выполнить разложение данных для удобства ICA (decompose data by ICA). В открывшемся окне (см. рис. 14) выбрать алгоритм (в данном случае – runica, основанный на Infomax, но есть также FastICA, SOBI, схожий с Runica – Binica и др).В commandline options выбираем: extended (необходим для обнаружения линейного шума), stop (матрица вращается, вычисляется разница с предыдущим шагом и когда она достигает порога, то матрица перестает вращаться),  lrate (по-другому называется learning rates, автоматический параметр, который задает скорость анализа данных), maxsteps (если порог, см. о нем в stop выше, не будет достигнут, то матрица в любом случае остановится через определенное количество шагов, например, 512), pca (чтобы уменьшить размерность).Нажимаем OK и алгоритм ICA запускается. На рис. 15 показаны изменения после проделанных шагов. Далее, чтобы изобразить полученные IC, кликаем на Plot – Component map и выбираем 2D/3D. В открывшемся окне (см. рис. 16) выбираем количество компонентов, которые хотим отобразить (в данном случае -12). Результат “хорошего” ICA показан на рис. 17, он будет иметь плавные переходы на топограммах, в отличие от “плохого” ICA, который будет похож на шахматную доску.  Чтобы посмотреть на записи полученный результат, нужно нажать на Component activations (scroll) в Plot (см. рис. 18). Чтобы увидеть свойства компонента здесь же, в Plot, выбрать Component properties (см. рис. 19). Чтобы посмотреть отдельно артефакт из записи ЭЭГ-сигнала нужно нажать на Inspect/label components by map, выбрать компонент (нажав на цифру рядом с scalp map) и здесь кликнуть на “Accept” (см. рис. 20). На рис. 21 показана классификация компонентов сигнала. Например, компонент 4 – типичный компонент, отображающий моргания глаз: на ERP-изображении видны отдельные точки, которые являются морганиями глаз (рис. 22). 

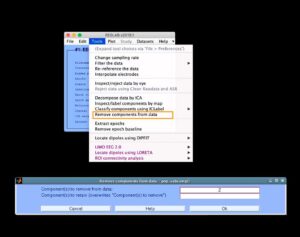
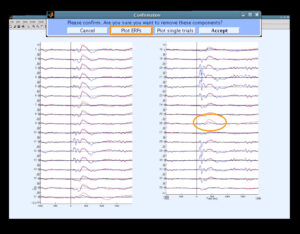
Удаление артефакта из данных производят так: нажать кнопку “Remove components from data”, в открывшемся окне выбрать количество компонентов, подлежащих удалению, и нажать OK (рис. 23). В окне “Confirmation” (см. рис. 24) выбираем Plot ERPs, при этом красным цветом будут показаны данные до удаления, а синим – после удаления. При выборе Plot single trials цвета меняются, то есть синий – до удаления, а красный – после.

Иллюстрации взяты из видео-лекции профессора Arnaud Delorme.6

Рисунок 14.  Для начала необходимо выполнить разложение данных для удобства ICA (decompose data by ICA)
Рисунок 15.  После этого мы можем наблюдать изменения между шагами
Рисунок 16. Чтобы изобразить полученные IC, кликаем на Plot – Component map и выбираем 2D/3D и выбираем количество компонентов
Рисунок 17. Результат “хорошего” ICA
Рисунок 18. Чтобы посмотреть на записи полученный результат, нужно нажать на Component activations (scroll) в Plot
Рисунок 19. Чтобы увидеть свойства компонента здесь же, в Plot, выбрать Component properties
Рисунок 20. Чтобы посмотреть отдельно артефакт из записи ЭЭГ-сигнала нужно нажать на Inspect/label components by map, выбрать компонент (нажав на цифру рядом с scalp map) и здесь кликнуть на “Accept”
Рисунок 21. Классификация компонентов
Рисунок 22. Компонент 4 – типичный компонент, отображающий моргания глаз
Рисунок 23. Удаление артефакта из данных
Рисунок 24. Результат удаления артефактов

Анализ ЭЭГ с использованием WICA/AWICA

Метод удаления артефактов WICA (wavelet independent component analysis) (wavelet independent component analysis) который основан на совместном применении дискретного вейвлет-преобразования и PCA. Метод подходит для удаления помех и артефактов в ЭЭГ. К недостатку этого метода можно отнести необходимость выбора зашумленных компонент в результатах вейвлет-преобразования. Существует автоматический вариант метода WICA – AWICA (automatic wavelet independent component analysis). Этот метод позволяет автоматически вырезать артефакты из многоканальных записей ЭЭГ. WICA показал хороший результат при работе с искусственно созданными записями ЭЭГ, в которых моделировались артефакты от электрического источника питания, помехи от мышечной активности и от моргания глаз.

Footnotes

  1. Tzyy-Ping Jung, C. Humphries, Te-Won Lee, S.Makeig, M. J. McKeown , V. Iragui , T. J. Sejnowski Removing Electroencephalographic Artifacts : Comparison between ICA and PCA // Neural Networks. – 1998. – №8.
  2. Акулов Л. Г., Муха Ю. П. Методы обработки электроэнцефалографических данных. [Электрон.ресурс] // ИЗВЕСТИЯ ВолгГТУ – 66 c. – 2008. – URL: http://www-dev.vstu.ru/files/vstu_periodical/1789/upload/2008-04.pdf#page=66
  3. A. Hyvärinen, E. Oja Independent Component Analysis: Algorithms and Applications // Neural Networks. – 2000. – №13. – С. 411-430.
  4. Izabela Rejer, Paweł Górski. Independent Component Analysis for EEG Data Preprocessing – Algorithms Comparison. 12th International Conference on Information Systems and Industrial Management (CISIM), Sep 2013, Krakow, Poland. pp.108-119.
  5. Izabela Rejer, Paweł Górski. Independent Component Analysis for EEG Data Preprocessing – Algorithms Comparison. 12th International Conference on Information Systems and Industrial Management (CISIM), Sep 2013, Krakow, Poland. pp.108-119.
  6. Arnaud Delorme, university professor at Paul Sabatier University in Toulouse // ICA applied to EEG part 7: Running ICA in EEGLAB and visualizing components // YouTube URL: https://www.youtube.com/watch?v=2hrYEYSycGI&list=PLXc9qfVbMMN2uDadxZ_OEsHjzcRtlLNxc&index=7 (дата обращения: 06.09.2020).