Метод главных компонент

Предварительный анализ медицинских данных в пространстве меньшей размерности. Метод главных компонент

Во многих задачах обработки и анализа биомедицинских данных исходное число р рассматриваемых, т.е. измеряемых на исследуемых объектах, признаков довольно велико. Для визуализации картины, простоты интерпретации и упрощения расчетов очень часто необходимо представить каждое из наблюдений в виде набора чисел, состоящего из существенно меньшего, чем р, числа признаков. При этом оставшиеся признаки могут либо выбираться из числа исходных, либо определяться по какому-либо правилу по совокупности исходных признаков, например, как линейные комбинации последних.

Главные компоненты представляют собой новое множество исследуемых признаков y⁽¹⁾, y⁽²⁾, … , y^(p) каждый из которых получен в результате некоторой линейной комбинации непосредственно измеренных на объектах исходных признаков x⁽¹⁾, x⁽²⁾, … , x^(p). Полученные в результате такого преобразования новые признаки y⁽¹⁾, y⁽²⁾, … , y^(p) могут обладать рядом удобных статистических свойств, например, быть упорядоченными по степени рассеяния в изучаемой совокупности объектов: первый признак обладает наибольшей степенью рассеяния, т. е. наибольшей дисперсией, второй — меньшей, и т. д.

Рассмотрим метод вычисления главных компонент¹. Будем предполагать, что исследуемые наблюдения Х₁, Х₂, …. Х_n извлечены из некоторой р мерной генеральной совокупности, определяемой соответствующей вероятностной мерой. Из всех характеристик исследуемой совокупности данных существенное значение имеет ковариационная матрица Σ = |σ_ij|, где

σ_ij = M (x⁽ⁱ⁾ – а⁽ⁱ⁾)(x^(j) — а^(j)), i, j = 1, 2…..р. (1.5)

Здесь а⁽ⁱ⁾— компоненты вектора а средних значений признаков x⁽ⁱ⁾. Будем считать, что в (1.5) а = 0. Этого всегда можно добиться, рассматривая в качестве исходных признаков x⁽¹⁾, x⁽²⁾, … , x^(p) не сами

измерения, а их отклонения от выборочных средних значений.

Первой главной компонентой исследуемой совокупности наблюдений называется такая нормированная линейная комбинация р исходных признаков x⁽¹⁾, x⁽²⁾, … , x^(p):

у⁽¹⁾=l₁₁x⁽¹⁾ + l₁₂x⁽²⁾ + … + l_1рx^(p)=L₁^TХ

(L₁^T = |l₁₁ l₁₂ … l₁_р|, l²₁₁+ l²₁₂+ … + l²_1p = 1), которая среди всех прочих нормированных линейных комбинаций обладает наибольшей дисперсией.

Вообще, i-й главной компонентой исследуемой генеральной совокупности (i = 1,3, …,р) называют такую нормированную линейную комбинацию р исходных признаков x⁽¹⁾, x⁽²⁾, … , x^(p)

у⁽ⁱ⁾=l_i1x⁽¹⁾ + l_i2x⁽²⁾ + … + l_iрx^(p)=L_i^TХ,

которая среди всех прочих линейных нормированных (l²_i1+ l²_i2+ … + l²_ip = 1) комбинаций, некоррелированных со всеми предшествующими главными компонентами y⁽¹⁾, … , y^(i-1) (т.е. cov(y⁽ⁱ⁾, y^(j⁾) = М(y⁽ⁱ⁾, y^(j⁾) = 0 для j < i), обладает наибольшей дисперсией.

Из определения следует, что, во-первых, главные компоненты y⁽¹⁾, y⁽²⁾, … , y^(p) пронумерованы в порядке убывания их дисперсий, т.е. D_y⁽¹⁾ ≥D_y⁽²⁾≥ … ≥ D_y^(p) , где

D_y⁽ⁱ⁾ = M(L_i^TX)² = M(L_i^TXX^TL_i)= L_i^TΣL_i, (1.6)

и, во-вторых, вектор L_i, определяющий переход от x⁽¹⁾, x⁽²⁾, … , x^(p)к у⁽ⁱ⁾, является i-м собственным вектором ковариационной матрицы Σ, т.е. его компоненты l_i1,l_i2, …, l_iропределяются как нормированное $\left(\sum_{j=1}^{p} l_{i j}^{2}=1\right)$ решение системы уравнений

(Σ-λ_iI)L_i =0. (1.7)

Эта система линейных однородных уравнений имеет ненулевое решение только в том случае, когда ее определитель равен нулю, т.е.

|Σ-λI|=0, (1.8)

где | • | означает определитель матрицы, λ — неизвестное число, I единичная матрица.

Выражение (1.8), в котором определитель матрицы (Σ-λI) является многочленом степени р относительно λ, называют характеристическим уравнением, а его корни λ_i, i = 1,2…..р собственными значениями матрицы Σ.

Каждому собственному значению λ_i, определяемому из (1.8), соответствует свой собственный вектор L_i, матрицы Σ. Составляющие этого вектора l_i1,l_i2, …, l_iр для конкретного значения λ_i, могут быть

найдены путем решения системы уравнений (1.7).

Из сопоставления (1.6)-(1.8) следует, что

D_у⁽ⁱ⁾ = L_i^TΣL_i = L_i^Tλ_iIL_i = λ_i.

Таким образом, ковариационная матрица Σ_Y главных компонент y⁽¹⁾, y⁽²⁾, … , y^(p) будет иметь вид диагональной матрицы

$\boldsymbol{\Sigma}_{Y}=\left[\begin{array}{ccccc}{\lambda_{1}} & {0} & {0} & {\ldots} & {0} \\ {0} & {\lambda_{2}} & {0} & {\ldots} & {0} \\ {\ldots} & {\ldots} & {\ldots} & {\ldots} & {\ldots} \\ {0} & {0} & {0} & {\ldots} & {\lambda_{p}}\end{array}\right]$

Учитывая, что преобразование, с помощью которого осуществляется переход от исходных компонент X к главным компонентам Y (Y = LX), является ортогональным, исходные переменные x⁽¹⁾, x⁽²⁾, … , x^(p) можно выразить через главные компоненты

x⁽ⁱ⁾=l_1iy⁽¹⁾ + l_2iy⁽²⁾ + … + l_рiy^(p)

(в матричной записи X = L ^T Y).

Несмотря на то, что для р исходных признаков получено р главных компонент, вклад большей их части в суммарную дисперсию оказывается небольшим. Поэтому, исключив из рассмотрения те компоненты, вклад которых мал, можно существенно сократить размерность исследуемого признакового пространства.

Ортогональное преобразование Y = LX оставляет инвариантной обобщенную дисперсию, а также сумму дисперсий компонент исходного вектора X и, как следствие, суммарная дисперсия (D_y⁽¹⁾ +D_y⁽²⁾+ … + D_y^(p) ) главных компонент, равная сумме собственных чисел (λ₁ + λ₂+ … + λ_р), также равна сумме дисперсий (D_x⁽¹⁾ +D_x⁽²⁾+ … + D_x^(p) ) исходных признаков². Па этом основании принимается решение о том, сколько последних главных компонент можно исключить из последующего рассмотрения. Для этого проводится анализ изменения относительной доли дисперсии

$q\left(p^{\prime}\right)=\frac{D y^{(1)}+D y^{(2)}+\ldots+D y^{\left(p^{\prime}\right)}}{D y^{(1)}+D y^{(2)}+\ldots+D y^{(p)}}=\frac{\lambda_{1}+\lambda_{2}+\ldots+\lambda_{p^{\prime}}}{\lambda_{1}+\lambda_{2}+\ldots+\lambda_{p}}$ (1.9)

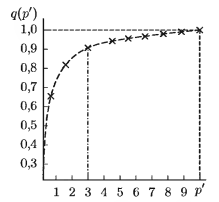
(1≤ p’ ≤ p), вносимой первыми p’ главными компонентами, и определяется число компонент, которое целесообразно сохранить. Так, для примера кривой q (p’) изображенной на рис. , очевидно возможно сокращение размерности пространства с р = 10 до р = 3. так как вклад семи последних главных компонент в суммарное рассеяние составляет не более 10 %.

Анализируя лишь p’ = 3 первых, т.е. наиболее весомых главных компонент, можно объяснить основную долю, а именно, 90 % суммарной дисперсии и выявить особенности рассеяния или группировки наблюдений.

Такой анализ главных компонент целесообразен, если величины x⁽¹⁾, x⁽²⁾, … , x^(p) являющиеся составляющими вектора X, имеют одинаковую размерность. В случае, если признаки x⁽¹⁾, x⁽²⁾, … , x^(p) измеряются в различных физических единицах, на этапе предобработки необходимо перейти к безразмерным признакам x^*(i) например, с помощью нормирующего преобразования вида

$x_{\nu}^{*(i)}=\frac{x_{\nu}^{(i)}}{\sqrt{\sigma_{i i}}} \quad(i=1,2, \ldots, p, \quad \nu=1,2, \ldots, n)$ ,

где σ_ijсоответствует (1.5), а затем вычислять главные компоненты относительно этих признаков x*⁽¹⁾, … , x*^(p) и их ковариационной матрицы.

Пример. Исходные данные представляют собой результат описания множества реализаций электрокардиограмм ЭКГ (ритмограмм) набором признаков x⁽¹⁾, x⁽²³⁾, x⁽³⁾, x⁽⁴⁾, x⁽⁵⁾. Эти признаки получены

в процессе вычисления и анализа параметров энтропии Колмогорова, которая отражает степень сложности (хаотичности) сигналов. Выборка данных включает несколько классов ЭКГ: мерцательная аритмия (МА), нормальный ритм (IIP), частая экстрасистолия (ЧЭ). Каждый класс представлен 25 объектами.

Требуется перейти от исходных признаков к главным компонентам, оценить долю дисперсии, которая обеспечивается первыми двумя главными компонентами (y⁽¹⁾, y⁽²⁾) , и отобразить объекты в пространстве новых признаков.

По данным измерений в соответствии с формулой (1.5) определена выборочная ковариационная матрица Σ — |σ_ij|

$\left[\begin{array}{rrrrr}{0,327} & {0,177} & {-4,359 \cdot 10^{-4}} & {-0,061} & {-0,085} \\ {0,177} & {0,112} & {0,018} & {-0,023} & {-0,052} \\ {-4,359 \cdot 10^{-4}} & {0,018} & {0,026} & {0,015} & {-1,636 \cdot 10^{-3}} \\ {-0,061} & {-0,023} & {0,015} & {0,022} & {0,016} \\ {-0,085} & {-0,052} & {-1,636 \cdot 10^{-3}} & {0,016} & {0,064}\end{array}\right]$

Решая в соответствии с (1.8) уравнение пятой степени относительно λ₁

$\left|\begin{array}{ccccc}{0,327-\lambda} & {0,177} & {-4,359 \cdot 10^{-4}} & {-0,061} & {-0,085} \\ {0,177} & {0,112-\lambda} & {0,018} & {-0,023} & {-0,052} \\ {-4,359 \cdot 10^{-4}} & {0,018} & {0,026-\lambda} & {0,015} & {-1,636 \cdot 10^{-3}} \\ {-0,061} & {-0,023} & {0,015} & {0,022-\lambda} & {0,016} \\ {-0,085} & {-0,052} & {-1,636 \cdot 10^{-3}} & {0,016} & {0,064-\lambda}\end{array}\right|=0$

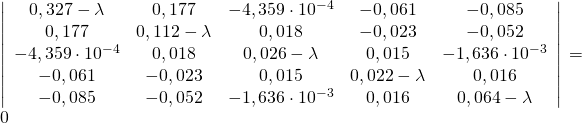
находим собственные значения λ₁ = 0,463; λ₂ = 0,047; λ₃ = 0,038; λ₄ = = 2,7 • 10^–³; λ₅ = 8,1*10 ^–⁴. Они упорядочены в порядке убывания их значений.

Подставляя последовательно численные значения λ₁, λ₂, λ₃, λ₄, λ₅ в систему уравнений (1.7) и решая ее относительно неизвестных L_i = [ l_i1l_i2 l_i3l_i4 l_i5]^T, i = 1, 2, 3, 4, 5, находим

$\left.\mathbf{L}_{1}=\left[\begin{array}{c}{-0,835} \\ {-0,469} \\ {-0,015} \\ {0,148} \\ {0,246}\end{array}\right], \left. \mathbf{L}_{2}=\left[\begin{array}{c}{-0,228} \\ {0,431} \\ {0,724} \\ {0,453} \\ {0,182}\end{array}\right], \left.\mathbf{L}_{3}=\left[\begin{array}{c}{0,217} \\ {0,132} \\ {0,172} \\ {0,089} \\ {0,947}\end{array}\right], \left.\mathbf{L}_{4}=\left[\begin{array}{c}{0,421} \\ {-0,575} \\ {0,018} \\ {0,696} \\ {-0,085}\end{array}\right], \left.\mathbf{L}_{5}=\left[\begin{array}{c}{0,162} \\ {-0,469} \\ {0,667} \\ {-0,53} \\ {-0,039}\end{array}\right]$

В качестве главных компонент получаем

y⁽¹⁾ = -0,84x⁽¹⁾ – 0,47x⁽²⁾ – 0,02x⁽³⁾ + 0,15x⁽⁴⁾ + 0,25x⁽⁵⁾,

y⁽²⁾ = -0,23x⁽¹⁾ +0,43x⁽²) + 0,72x⁽³⁾ + 0,45x⁽⁴⁾ – 0,18x⁽⁵⁾,

y⁽³⁾ = 0,22x⁽¹⁾ + 0,13x⁽²⁾ + 0,17x⁽³⁾ + 0,09x⁽⁴⁾ + 0,95x⁽⁵⁾,

y⁽⁴⁾ = 0,42x⁽¹⁾ – 0,57x⁽²⁾ = 0,02x⁽³⁾ + 0,70x⁽⁴⁾ – 0,08x⁽⁵),

y⁽⁵⁾ = 0,16x⁽¹⁾ – 0,47x⁽²⁾ + 0,67x⁽³⁾ – 0,53x⁽⁴⁾ – 0,04x⁽⁵⁾.

Здесь под x⁽¹⁾, x⁽²⁾, x⁽³⁾, x⁽⁴⁾, x⁽⁵⁾ подразумеваются отклонения параметров энтропии от их средних значений.

Вычисление относительной доли суммарной дисперсии, обусловленной пятью главными компонентами, в соответствии с формулой (1.9) дает следующие результаты:

$q(1)=\frac{\lambda_{1}}{\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}+\lambda_{5}}=0,84$
$q(2)=\frac{\lambda_{1}+\lambda_{2}}{\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}+\lambda_{5}}=0,925$
$q(3)=\frac{\lambda_{1}+\lambda_{2}+\lambda_{3}}{\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}+\lambda_{5}}=0,994$
$q(4)=\frac{\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}}{\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}+\lambda_{5}}=0,999$
$q(5)=1$

По результатам вычислений можно сделать вывод о том, что почти вся информация (92,5 %) об изменчивости энтропийных характеристик наблюдаемой выборки ЭКГ-данных (75 объектов) содержится в первых двух главных компонентах.

Па рис.2 приведено изображение множества ритмограмм в пространстве двух первых главных компонент для трех классов ЭКГ (МЛ, HP, ЧЭ).

Рис. 1. Представление ритмограмм классов: мерцательная аритмия (МА), нормальный ритм (ПР) и частая экстрасистолия (ЧЭ), в пространстве двух первых главных компонент

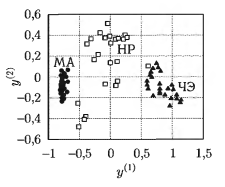
Рис. 2. Пример построения линейной дискриминантной функции

Как видно из рисунка, описание объектов параметрами энтропии позволяет получить группировку объектов, соответствующую трем классам рассматриваемых ЭКГ-сигналов. Наиболее плотная группировка объектов наблюдается в классе МЛ. Возможно линейное разделение классов, причем, используя энтропийные характеристики ритмограмм, можно эффективно решить задачу распознавания опасного нарушения (МА) на фоне альтернативных групп аритмий (ЧЭ и HP с выраженной дыхательной аритмией).

Метод главных компонент для удаления шума

Метод главных компонент находит применение при компрессии изображений и видео для уменьшения пространственной избыточности пикселей при кодировании изображений и видео, когда используются линейные преобразования блоков пикселей. Также метод используется и при обработке биомедицинских сигналов, таких как ЭЭГ.

Метод главных компонент решает следующие задачи:

Очищение сигнала от шумов.
Локализация основных частот сигнала

При удалении шума из сигнала необходимо представить данные в многомерном пространстве, применить к нему метод главных компонент и оставить только первые компоненты преобразования. При этом предполагается, что в первых компонентах содержится основная полезная информация, оставшиеся же компоненты содержат ненужный шум.

Преимущество данного метода состоит в том, что метод не требует от пользователя заданную точность. Целевой подход к оценке числа главных компонент по необходимой доле объяснённой дисперсии формально применим всегда. Однако, где нет разделения на «сигнал» и «шум» любая заранее заданная точность имеет смысл. Таким образом, «сигнал» предполагает сравнительно малую размерность при относительно большой амплитуде. «Шум» предполагает большую размерность при относительно малой амплитуде. С этой точки зрения метод главных компонент работает как фильтр: сигнал содержится в основном в проекции на первые главные компоненты, а в остальных компонентах пропорция шума намного выше.

Footnotes

Айвазян С. А., Бежаева 3. И., Староверов О. В. Классификация многомерных наблюдений. — М.: Статистика, 1974. – 240 с.
Айвазян С. А., Ьежаева 3. И., Староверов О. В. Классификация многомерных наблюдений. — М.: Статистика, 1974. – 240 с.