Аппроксимированная энтропия

Распознавание биосигналов с нелинейными свойствами по параметрам аппроксимированной энтропии

Методы нелинейной динамики все шире используют в практических задачах анализа сложных биомедицинских сигналов (ЭЭГ, ЭКГ, ритм сердечных сокращений и др.). Такие сигналы при определенных условиях можно рассматривать как процессы, генерируемые режимом динамического хаоса. Это представление значительно расширяет спектр количественных критериев для диагностики состояний, поскольку основано на анализе характеристик, применяемых для исследования детерминированного хаоса. Так, например, в работах¹² в качестве такого критерия предложено использовать аппроксимированную энтропию (Approximate Entropy — АрЕп), которая количественно определяет степень сложности сигнала.

Аппроксимированная энтропия тесно связана с энтропией Колмогорова (К-энтропией), которая считается важнейшей характеристикой хаотического движения в фазовом пространстве произвольной размерности³. К-энтропия определяется как средняя скорость потери информации о состоянии динамической системы во времени. При этом для описания состояния системы вводится понятие аттрактора, под которым понимается множество точек или подпространств в фазовом пространстве (образованном компонентами вектора состояний Х(/)), к которому приближаются хаотические траектории⁴. Предполагается, что d-мерное фазовое пространство разделено на ячейки размером r^d, а состояние системы X(t) определяется дискретно через интервалы времени τ. Поведение системы на странном аттракторе (аттракторе, имеющем фрактальную размерность) оценивается в виде дополнительной информации, необходимой для предсказания того, в какой ячейке i*_m+1 фазового пространства будет находиться система в момент времени t_m+1, если известно, что на предыдущих шагах она находилась на траектории i*₁, i*₂, …i*_m. K-энтропия равна нулю для регулярного движения, бесконечна для случайных систем, положительна и постоянна для систем с детерминированным хаосом. Анализируя некоторый сигнал, кажущийся случайным, можно отличить нерегулярность, связанную с динамикой движения на аттракторе, от воздействия на систему белого шума.

На практике значение К-энтропии сложно вычислить ввиду того, что анализируется одна реализация сложного процесса, хотя аттрактор, характеризующий свойства системы, вложен в d-мерное фазовое пространство. Однако в соответствии с теоремой Таксиса некоторые свойства аттрактора можно восстановить по одной составляющей процесса. При этом можно найти нижнюю границу K-энтропии

$K_{2}=-\lim _{r \rightarrow 0} \lim _{m \rightarrow \infty} \frac{1}{m} \ln \frac{C_{m}(r)}{C_{m+1}(r)}$ (2.8)

где C_m(r) — обобщенный корреляционный интеграл; m — длина последовательности точек; r — пороговое расстояние.

Корреляционный интеграл вычисляется в виде

$C_{m}(r)=\lim _{N \rightarrow \infty} \frac{1}{N^{2}} \sum_{i}^{N} \sum_{j}^{N} \Theta(r-|X(i)-X(j)|), \quad i \neq j$ (2.9)

где X(i) = (х(i), x(i + I), …. x(i +m- 1)) — последовательность, состоящая из m отсчетов сигнала; Θ(•) функция Хевисайда (Θ(s) = 1, если s > 0, и Θ(s) = 0, если s < 0); N — объем выборки данных.

Если показатель K₂> 0. то зто означает достаточное условие существования хаоса. Однако требование m → ∞, r → ∞, N → ∞ в (2.7), (2.8) делает невозможным применение критерия K₂ в практических задачах анализа сигнала на конечных выборках. Это приводит к необходимости нахождения приближенной оценки энтропии Колмогорова в виде аппроксимированной энтропии.

Рассмотрим алгоритм вычисления функции аппроксимированной энтропии.

Алгоритм вычисления функции аппроксимированной энтропии

Пусть имеется выборка исходных данных x(1), х(2)…..x(N) где N — длина выборки. Вначале зададим значения двух параметров: m — длина анализируемых цепочек (последовательностей отсчетов), r порог, задающий размеры ячеек фазового пространства.

Формируем последовательности X(i), …..X(N – m + 1), определяемые выражением: X(i) = (x(i), x(i + I)…..x(i + m – 1)), i =1…..X(N – m + 1).

Определяем расстояние между X(i) и X(j) как

$d (X(i), X(y))=& \max _{k=0, ...,(m-1)} (|x(i+k)-x(j+k)|)$

Вычисляем C_r^m(i)=N^m(i)/(N–m+1), где N^m(i) количество значений d(X(i), X(j)), удовлетворяющих условию d(X(i), X(j)) ≤ r; j = 1…..(N –m+1).

Находим натуральный логарифм от каждого C_r^m(i) и усредняем его значение по индексу i: $\theta^{m}(r)=\frac{1}{N-m+1} \sum_{i=1}^{N-m+1} \ln C_{r}^{m}(i)$

Увеличиваем значение m до m + 1. Повторяем шаги 1-4 и находим значения C_r^m+1(i), θ^m+1(r).
Находим оценку K-энтропии

$ApEn(m,r)=\lim _{N \rightarrow \infty} (\theta^{m}(r)-theta^{m+1}(r))$

которая для выборки данных ограниченной длины принимает вид

ApEn(m,r,N) = (θ^m(r) – θ^m+1(r)).

В работе⁵ был предложен быстродействующий алгоритм вычисления этой оценки.

Значение аппроксимированной энтропии зависит от параметров m и r. Пинкус предложил принять значение m = 2 и r равным (0,1, …, 0,25)σ_х, где σ_х — стандартное отклонение исходной выборки данных ⁶. Все последующие расчеты аппроксимированной энтропии проведены для N = 300, m = 1, …, 6 и r = 0,15σ_х.

Сложность анализа аппроксимированной энтропии как функции длины анализируемых цепочек m при конечной длине выборки N связана с тем, что при возрастании m значение ApEn(m) стремится к нулю независимо от степени регулярности исследуемого процесса. Это происходит из-за увеличения вероятности того, что цепочки длиной m будут представлять собой лишь однажды произошедшие события. По этой причине аппроксимированная энтропия, вычисленная в соответствии с многошаговой процедурой, дает ошибочную оценку степени хаотичности сигнала. Избежать этого можно, вводя коррекцию оценки ApEn(m)⁷⁸⁹:

ApEn_с0r(m) = ApEn(m) + ApEn(0)N⁽¹⁾_m/N_m+1, (2.10)

где N_m+1~ число анализируемых цепочек длины (m + 1); N⁽¹⁾_m -число лишь однажды встретившихся цепочек длиной m; АрЕп(0) — значение абсолютной энтропии, вычисленное для исходной последовательности отсчетов.

При этом нижнюю границу К-энтропии можно аппроксимировать нижней оценкой ApEn_с0r(m). Отметим, что вид коррекции (2.9) аналогичен корректирующей оценке (2.6). используемой при анализе условной энтропии Шеннона.

Основное отличие аппроксимированной энтропии от условной энтропии E(L/L— 1) заключается в способе формирования элементарных областей фазового пространства. При расчете условной энтропии гиперкубы формируются жесткой сеткой, задаваемой числом уровней квантования ξ в пределах минимального и максимального значений (x_min, x_max) временного ряда. При расчете ApEn(m) работает механизм адаптивного формирования элементарных областей путем построения гиперсфер радиусом r с центром, задаваемым каждой точкой, в которой находится объект фазового пространства. Схематическое изображение механизмов формирования элементарных ячеек для двумерного пространства приведено на рис. 1.

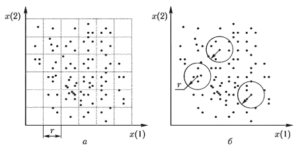
Рис. 1. Иллюстрация механизма формирования ячеек фазового пространства при расчете: а условной энтропии, б — аппроксимированной энтропии

Анализ свойств и выбор параметров аппроксимированной энтропии

В работах¹⁰¹¹¹² проведены модельные эксперименты, направленные на исследование свойств аппроксимированной энтропии. Среди основных свойств этой характеристики можно выделить следующие.

Аппроксимированная энтропия отражает степень сложности сигнала — чем выше его регулярность, тем меньше значение этой величины.
Она позволяет получать надежные оценки хаотических свойств сигналов, используя короткие выборки данных.

Результаты экспериментов показали, что как для длинных, так и для более коротких последовательностей получаются устойчивые оценки энтропии. В дальнейшем было решено анализировать фрагменты сигналов длиной N = 300 отсч.

Приближенная оценка Д-энтропии может использоваться для обнаружения динамических нерегулярностей, связанных как с нелинейными, так и со стохастическими свойствами сигналов.

В качестве примера на рис. 2 приведены результаты вычисления АрЕn(m) и ApEn_cor(m) для логистического отображения¹³, определяемого в виде: Х(i + 1) = а • Х(i)(1 – Х(i)). где а — внешний параметр. Данное отображение представляет собой простейшее нелинейное разностное уравнение, которое при а = 3,5 имеет периодический характер (рис. 2, а), а при а = 3,8 — хаотический (рис. 2, в). На представленных графиках наблюдаются отличия полученных характеристик, а именно: при а = 3,5 АрЕn(m) с ростом m быстро уменьшается до нуля (рис. 2, б), что характерно для периодических сигналов, а введение коррекции не вносит изменений в оценку ApEn_cor(m) (графики зависимостей совпадают). В то же время, при переходе к режиму детерминированного хаоса (а = 3,8) зависимость АрЕn(m) с ростом m стремится не к нулю, а к некоторому постоянному уровню (рис. 2, г). При этом на шаге m = 5 включается корректирующая поправка, что вызвано возрастанием числа одиночных цепочек, обнаруженных при анализе элементарных гиперсфер.

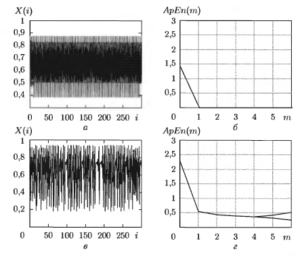
Рис. 2. Логистическое отображение при а = 3,5 и а = 3,8
а и в исходный сигнал X(i); б и г — зависимости АрЕп(m) (сплошная линия) и ApEncor(m) (пунктирная линия) от m

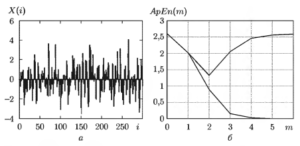
Рис. 3. Авторегрессионный процесс 2-го порядка
а — исходный сигнал X(i); б — зависимость ApEn(m) (сплошная линия) и ApEncor(m)) (пунктирная линия) от m

Рис. 4. Зависимость АрЕn(m) от амплитуды шума

При анализе стохастического процесса вид кривых АрЕn(m) и ApEn_cor(m) резко изменяется. На рис. 3 представлен результат анализа процесса авторегрессии второго порядка, который задан следующим уравнением:

X(i) – μ = a₁(Х(i – 1) – μ) + a₂(X(i – 2) – μ) 4- Z(i), где μ — математическое ожидание случайной величины Z(i); Z(i), i = 1, 2, … — белый шум с нормальным законом распределения; a₁ = 1,0, а₂ = -0,5.

Как видно из рис. 3, б, на графиках наблюдается ярко выраженный минимум ApEn_cor(m), значения ApEn(m) при малых m достаточно велики, а при возрастании m стремятся к нулю, в то время как функция ApEn_cor(m) — к значению абсолютной энтропии ApEn(0). Характер зависимостей ApEn(m) и ApEn_cor(m) аналогичен закономерностям, выявленным для случая белого шума.

Приближенная оценка К-энтропии применима для анализа как детерминированных хаотических процессов, так и стохастических сигналов. Более того, она позволяет оценить степень зашумленности детерминированного сигнала в смешанном процессе, что является свойством, полезным для анализа биосигналов, поскольку многие из них содержат как регулярную, так и стохастическую составляющие.

Нечувствительность аппроксимированной энтропии к воздействию белого шума определяется выбором подходящего значения порога r. Если величина r больше амплитуды шума, то его влияние будет эффективно устранено.

Проиллюстрируем это следующим примером¹⁴. Пусть наблюдается смешанный процесс X(i) = s(i) + cn(i), где s(i) = 3cos(π/20); i=1…..N— гармонический сигнал; n(i) — шум, равномерно распределенный в пределах значений ( -1, +1); с – коэффициент, задающий амплитуду шумовой составляющей сигнала.

Как видно из рис. 4, значения ApEn(m) при всех m, кроме m = 1, помехоустойчивы. При с < r (r = 0,32) значения ApEn(m = 2, … . …6) постоянны и увеличиваются с ростом m лишь в случае, когда амплитуда шума превысит значение заданного порога r.

Аппроксимированная энтропия нечувствительна к изменению частоты гармонического сигнала.

Исходя из анализа свойств аппроксимированной энтропии и результатов модельных экспериментов, можно сделать вывод о том, что для оценки степени регулярности изменений, наблюдаемых в дискретной последовательности отсчетов, могут быть использованы следующие параметры:

значения ApEn(m) и ApEn_cor(m) при m = 1,2, 3, где вклад одиночных цепочек незначителен;
относительный минимум ApEn_cor(m):

МЕ_К = АрЕn(0) – min {ApEn_cor(m)}, который аппроксимирует нижнюю границу К-энтропии.

Распознавание мерцательной аритмии

Эти параметры были использованы для распознавания мерцательной аритмии по последовательности кардиоинтервалов¹⁵¹⁶. Анализ корреляционной размерности ритмограмм при мерцательной аритмии (МЛ) показал¹⁷, что сердечный ритм имеет хаотическую природу и, следовательно, в этой задаче применимы методы нелинейной динамики. Все исследования проведены на ритмограммах реальных записей электрокардиосигнала. Реализации ЭКГ пациентов были выбраны из базы архивных записей пациентов 4-го кардиологического отделения СПб ГУЗ «Городская больница № 31». Все реализации были предварительно верифицированы и разделены на 3 класса: нормальный ритм (HP), включающий выраженную дыхательную аритмию; мерцательная аритмия (МЛ); частая экстрасистолия (ЧЭ). Затем в каждой из трех групп были отобраны наиболее характерные для данного класса реализации (по 50 реализаций длиной 300 отсч.) и сформированы обучающие выборки. Для этих фрагментов из обучающей выборки были рассчитаны значения АрЕn(m) и ApEn_cor(m) для m = 1, …,6, а также МЕ_к.

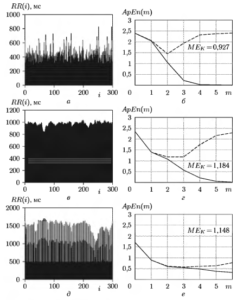
Рис. 5. Примеры оценок АрЕn(m) (сплошная линия) и ApEncor(m) (штриховая линия) для реальных сигналов
а, б — мерцательной аритмии; в, г — нормального ритма; д, е — частой экстрасистолии

На рис. 5 приведены примеры ритмограмм и полученные зависимости АрЕn(m) от длины цепочек m для классов МА (а, б), HP (в, г) и ЧЭ (д, е) при r₀ = 0,15. r= r₀σ_х. Как видно из рисунка, зависимости имеют различный характер, причем МА характеризуется наименьшим значением МЕ_к.

Построение решающих функций по оценкам аппроксимированной энтропии выполнено с использованием теории линейного дискриминантного анализа. Задача распознавани МА предполагает обнаружение аритмии на фоне других нарушений ритма, поэтому дискриминантный анализ был проведен для двухклассовой задачи: один класс составили ритмограммы МА (класс w₁), в другой класс были объедены реализации HP и ЧЭ (класса w₂). Классификация осуществлялась с использованием различною набора признаков, в качестве которых были выбраны параметры АрЕn(m) и ApEn_cor(m).

Уравнение линейной разделяющей функции в пространстве заданных признаков определялось в виде D(X) = W^T • X + w₀ = 0, где W = [w₁,w₂ … w_d]^T — весовой вектор единичной длины; X = |x₁,x₂ … x_d|^T — вектор наблюдений; d — число признаков; w₀ — пороговая величина.

Значение порога w₀ определялось исходя из критерия оптимальности разбиения на классы, т.е. минимизации суммы ошибок первого рода α (ложная тревога) и второго рода β (пропуск цели): (α + β) → min, поскольку в этом случае одинаково важно как не пропустить МA, так и не выдать сигнал ложной тревоги.

Для нахождения ошибок α и β были построены гистограммы распределения проекций объектов на единичный вектор W, а также соответствующие этим гистограммам функции плотности распределения, имеющие нормальный закон распределения. Величина порога фильтрации r была задана, равной r= r₀σ_х, r₀ = 0,2, что увеличило число оцениваемых параметров АрЕn(m) до m 6. Выбор информативных признаков осуществлялся по кривой зависимости критерия Фишера J от числа параметров, включенных в решающее правило. Это позволило ограничить описание объектов, используемое для распознавания классов w₁,w₂, следующим набором признаков: МЕ_к; АрЕn(m) при m= 1, 2, 3. Эксперименты по оценке эффективности решающих правил показали, что в этом случае теоретические ошибки классификации минимальны и составляют менее 0,1 %. Эффективность решающего правила проверена на контрольной выборке, включающей по 100 реализаций ЭКГ для каждого из трех видов ритма (МA класс w₁, HP и ЧЭ класс w₂). Как показали результаты расчетов, данный метод обладает высоким уровнем чувствительности (S_c =0,98) и специфичности (S_p = 0,985) при распознавании МЛ. Полученные данные (метод АрЕn) сравнивались с результатами обнаружения МЛ, использующими альтернативные методы распознавания¹⁸¹⁹²⁰:

проверка гипотезы о гауссовом законе распределения (Критерий хг);
оценка среднеквадратического отклонения ритмограммы (Dev);
предсказание авторегрессионной моделью (AR-модель);
оценка минимума уточненной условной энтропии (ME).

В этих методах используется лишь один информативный признак, являющийся индикатором приступов МЛ. Результаты анализа эффективности этих методов приведены в табл.

Таблица

Метод	Условия обнаружения МA — на фоне	Чувствительность метода, S_c, %	Специфичность метода, S_p, %
Критерий	HP	74,5	97,4
Dev	ЧЭ	98,8	64,7
AR-модeль	HP и ЧЭ	93.3	91,4
ME	HP и ЧЭ	98,5	89,3
AрЕn	HP и ЧЭ	98.0	98.5

Из данных таблицы следует, что метод распознавания МЛ на основе аппроксимированной энтропии является наиболее надежным, что позволяет использовать его в практических задачах.

Footnotes

Nonlinear biomedical signal processing / ed. by Metin Akay. Vol. 2. Dynamic analysis and modelling. — New York: IEEE, 2001. — 341 p.
Pincus S. M. Approximate entropy as a measure of sytem complexity // Proc. Natl. Acad. Sci. USA 88: 1991. P. 2297 2301.
Шустер Г. Детерминированный хаос: Введение. М.: Мир, 1988. 240 с.
Мун Ф. Хаотические колебания: Вводный курс для научных работников и инженеров / Пер. с англ. — М.: Мир, 1990. — 312 с.
Nonlinear biomedical signal processing / ed. by Metin Akay. Vol. 2. Dynamic analysis and modelling. — New York: IEEE, 2001. — 341 p.
Pincus S. M. Approximate entropy as a measure of sytem complexity // Proc. Natl. Acad. Sci. USA 88: 1991. P. 2297 2301.
Манило Л. А., Зозуля Е. П. Исследование возможности применения аппроксимированной энтропии для анализа биосигналов // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. 2007. Вып. I. С. 3-9.
Манило Л. А., Немирно А. П. Аппроксимация энтропии Колмогорова при анализе хаотических процессов на конечных выборках // Математические методы распознавания образов ММРО-14: 14-я Всерос. конф. Владимирская обл., г. Суздаль. 21 26 сект. 2008) г.: сб. докл. – М.: МАКС Пресс, 2009. С. 405 407.
Манило Л. А. Распознавание фибрилляции предсердий в кардиологических системах диагностики и наблюдения // Биотехносфера. 2009, № 2. С. 41 45.
Nonlinear biomedical signal processing / ed. by Metin Akay. Vol. 2. Dynamic analysis and modelling. — New York: IEEE, 2001. — 341 p.
Манило Л. А., Зозуля Е. П. Исследование возможности применения аппроксимированной энтропии для анализа биосигналов // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. 2007. Вып. I. С. 3-9.
Манило Л. А., Немирно А. П. Аппроксимация энтропии Колмогорова при анализе хаотических процессов на конечных выборках // Математические методы распознавания образов ММРО-14: 14-я Всерос. конф. Владимирская обл., г. Суздаль. 21 26 сект. 2008) г.: сб. докл. – М.: МАКС Пресс, 2009. С. 405 407.
Шустер Г. Детерминированный хаос: Введение. М.: Мир, 1988. 240 с.
Nonlinear biomedical signal processing / ed. by Metin Akay. Vol. 2. Dynamic analysis and modelling. — New York: IEEE, 2001. — 341 p.
Манило Л. А. Распознавание фибрилляции предсердий в кардиологических системах диагностики и наблюдения // Биотехносфера. 2009, № 2. С. 41 45.
Манило Л. А., Зозуля Е. П. Автоматическое распознавание мерцательной арпмин с использованием оценок аппроксимированной энтропии И Информационно-управляющие системы. 2006, № 1 (20). С. 21-27.
Манило Л. А., Зозуля Е. П. Оценка корреляционной размерности временных рядов в задачах анализа аритмий // Биомедицинская радиоэлектроника. 2009, № 11. С. 32-39
Манило Л. А., Зозуля Е. П. Автоматическое распознавание мерцательной арпмин с использованием оценок аппроксимированной энтропии И Информационно-управляющие системы. 2006, № 1 (20). С. 21-27.
Манило J1. А. Автоматический анализ электрокардиосигнала в задачах распознавания нарушений сердечного ритма // Биотехнические системы в медицине и биологии / Под общ. ред. проф. Е. П. Попечителева. -СПб.: Политехника, 2002. — С. 6168.
Манило J1. А. Авторегрессионные модели случайных процессов в задачах распознавания нарушений сердечного ритма // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. 2004. Вып. 2. С. 1-8.