Непараметрические методы обучения (алгоритм персептрона)
Рассмотрим задачу нахождения линейной разделяющей границы для двух классов объектов w1 и w2. Предположим, что для обучения имеется N объектов обоих классов. Обозначим это множество объектов через Ψ. Множество Ψ состоит из двух обучающих выборок Ψ1 (объекты первого класса w1) и Ψ2 (объекты второго класса w2). Будем предполагать, что существует линейная функция, разделяющая Ψ1 и Ψ2 (т.е. Ψ1 и Ψ2 линейно разделимы).
Линейное решающее правило, разделяющее в n-мерном пространстве Ψ1 и Ψ2. как было показано ранее, имеет вид (1.2)
![]()
где x1,x2, … , xn — компоненты вектора объекта X = (x1,x2, … , xn). Добавим к ранее введенному вектору-объекту X (n + 1)-ю компоненту, равную 1, и обозначим такой расширенный вектор-объект через Y = (y1,y2, … , yn), где yi = xi для i = 1,…..,n, yn+1 = 1. Тогда обучающим выборкам Ψ1 и Ψ2 будут соответствовать обучающие выборки v1 и v2— множества соответствующих расширенных векторов. Их объединение обозначим через v.
В этом случае решающее правило будет иметь вид
![]()
или в векторной форме WTY = 0.
Предположение о линейной разделимости Ψ1 и Ψ2 означает, что существует вектор W, называемый решающим весовым вектором, такой, что
WTY > 0 для каждого Y ∈ v1,
WTY < 0 для каждого Y ∈ v2
Если все образы из v2 умножить на -1, то вышеприведенное условие запишется в виде
WTY > 0 для каждого Y ∈ v.
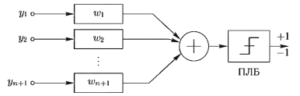
При таком представлении классификатор на два класса можно изобразить в виде рис. 7. Это — схема персептрона. Обучение такого классификатора на обучающем множестве v заключается в подборе таких значений компонент весового вектора W = (w1, w2, … , wn+1), чтобы при предъявлении на входе любого Y ∈ v1 на выходе появлялось бы +1, а при появлении любого Y ∈ v2 на выходе было бы -1.
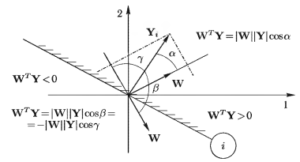
Каждому Y ∈ v можно поставить в соответствие плоскость (плоскость объекта) в этом же пространстве, которая проходит через начало координат и перпендикулярна Y. Ответ порогового логического блока зависит от того, с какой стороны от плоскости объекта находится точка W, как показано на рис. 8.
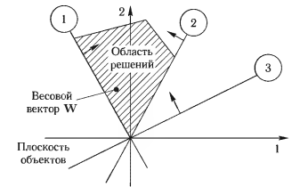
Будем считать, что при правильной классификации объектов из обучающей выборки v (с учетом изменения знака на противоположный у всех объектов из v2) ответ ПЛБ должен быть всегда положителен. Тогда для N объектов Y ∈ v можно построить N плоскостей и по ним определить некоторую область решений, как показано на рис. 9. Для любого W из этой области решений для всех объектов mby = v будет выполняться
WTY > 0.
Процедуры последовательного обучения с коррекцией ошибок
Можно по N обучающим объектам найти область решений и вы брать W внутри этой области. Мы рассмотрим иную процедуру последовательного обучения123, когда обучающие объекты предъявляются последовательно, по одному, а весовой вектор W уточняется с каждым новым входным вектором Y. В этом случае, если после предъявления объекта Y ∈ v выполняется WTY > 0, то W остается неизменным. Если же WT < 0, то вычисляется новое значение W, равное W’, по формуле
W’ = W + cY,
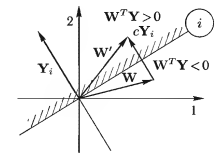
где с > 0 называется коэффициентом коррекции. Из этого выражения видно, что новое значение весового вектора выбирается на нормали к плоскости объекта, в ту сторону, где как показано на рис. 10.
Объекты предъявляются либо циклически, либо в случайном порядке до тех пор пока не повторится результат испытания каждого из них. Начальное значение W произвольно.
Рассмотрим три варианта алгоритма обучения в зависимости от процедуры выбора величины с.
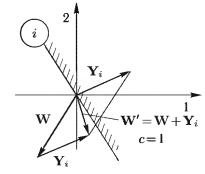
Если выбирается с = 1, то W’ = W + Y. Этот алгоритм с постоянным коэффициентом в зависимости от отношения величин WTY и с исправляет или не исправляет ошибку, произошедшую на данном объекте, как показано на рис. 11, так как W перемещается всегда на фиксированную величину, которая может быть больше или меньше расстояния W до плоскости объекта.
Для алгоритма с абсолютной коррекцией величина с выбирается заново на каждом шаге предъявления объекта Y, причем значение с выбирается как наименьшее целое число, которое делает величину WTY большей нуля, т. с. выбирается из условия
WTY = (W + cY)TY > 0.
При этом W перемещается перпендикулярно плоскости объекта на величину, чуть большую расстояния от W до этой плоскости. Если Y расположен на плоскости объекта, то из вышеприведенного выражения следует, что
(W + cY)T = WTY + cYTY = 0, WTY = -cYTY, |WTY| = |cYTY| = c|Y|2,
![]()
Поэтому с должно быть наименьшим целым числом, при этом большим, чем
![]()
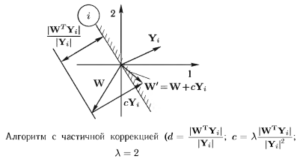
После корректировки весов по этому правилу на данном шаге классификатор будет правильно распознавать предъявленный объект Y (рис. 12).
Очевидно, что этот алгоритм приводит к гем же результатам, что и предыдущий алгоритм с постоянным коэффициентом при с = 1, если при использовании этого алгоритма объект предъявляется повторно до тех пор, пока он не будет правильно распознан.
Алгоритм с частичной коррекцией перемещает весовой вектор на расстояние, пропорциональное расстоянию от точки до плоскости, т. е. величине ![]() . Если новую точку выбирать на нормали к плоскости на расстоянии, пропорциональном этой величине, то
. Если новую точку выбирать на нормали к плоскости на расстоянии, пропорциональном этой величине, то
![]() .
.
где λ > 0 — коэффициент пропорциональности. Тогда
|Y| • |W’- W| = А • |WTY|.
Так как векторы Y и W’ – W коллинеарны, то из последнего равенства следует
| YT(W’— W)| = λ • |WTY|.
Так как W’ -W = cY, то |W’ – W| = |cY|, и поэтому |Y||cY| =λ |WTY| и
![]()
откуда
![]()
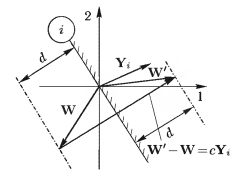
Коэффициент λ выбирается в диапазоне 0 < λ < 2. В случае λ = 0 весовой вектор вообще не изменяет положения, для λ = 1 вектор W переводится в W’, расположенный непосредственно на плоскости объекта, а при λ = 2 весовая точка переводится по другую сторону плоскости на расстояние, равное исходному расстоянию W до плоскости (рис. 13).
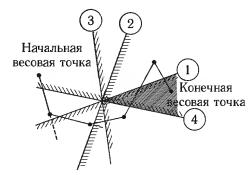
В общем случае алгоритм обучения с коррекцией ошибок заключается в последовательном испытании множества плоскостей объектов. Для каждой плоскости выясняется, лежит ли весовая точка по нужную сторону. Если это расположение неправильно, то весовая точка перемещается перпендикулярно плоскости по направлению к ней. Процесс продолжается до тех пор, пока не будет получен разделяющий весовой вектор (рис. 14). В теории доказывается4, что все три алгоритма сходятся за конечное число шагов.
Footnotes
- Рангайян Р. М. Анализ биомедицинских сигналов. Практический подход / Пер. с англ. А. II. Калиниченко; Под ред. Л. П. Немирно. -М.: Физматлит, 2007. — 440 с.
- Нильсон Н. Обучающиеся машины / Пер. с англ. — М.: Мир, 1967. -180 с.
- Васильев В. И. Распознающие системы. — Киев: Наукова думка, 1983. — 422 с.
- Нильсон Н. Обучающиеся машины / Пер. с англ. — М.: Мир, 1967. -180 с.