Методы распознавания образов применяются для задач анализа данных, которые характеризуются малым числом объектов в классах и для которых важно определить степень сходства или различия классов. Часто необходимо создать алгоритм автоматического определения (распознавания) принадлежности объектов к определенным классам. Распознавание образов относится к автоматизации интеллектуальных задач принятия решений и опирается на теорию вероятностей, теорию матриц, математическую логику и математическую лингвистику. Методам распознавания образов посвящена обширная литература12345 .
Можно привести следующие примеры применения методов распознавания образов в различных областях человеческой деятельности:
- диагностика заболеваний67;
- распознавание и прогнозирование угрожающих жизни состояний больного, психофизиологических состояний человека по комплексу электрофизиологических показателей8;
- автоматический анализ и интерпретация биомедицинских сигналов и изображений910;
- другие задачи: машинное зрение; распознавание речи; идентификация человека по голосу, отпечаткам пальцев, изображению глаза; чтение печатного и рукописного текста, топографических карт и т. п.
Представление образов в многомерном пространстве признаков
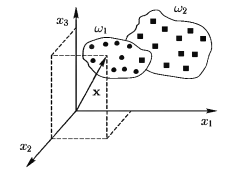
Допустим, мы имеем m классов объектов w1,w2,.., wm . Каждый поступающий объект должен быть отнесен к одному из этих m классов и каждый объект описывается набором из n измерений (действительных чисел) x1, x2,…,хn, которые называются признаками. Такой набор может быть представлен точкой в n-мерном евклидовом пространстве или, иначе говоря, вектором признаков X = (x1, x2,…,хn) в n-мерном признаковом пространстве, где x1, x2,…,хn — декартовы координаты конца вектора X. Например, при диагностике состояний больного мы имеем 2 класса: w1 — A-состояние, w2 — В-состояние.
Каждый поступающий больной описывается 3 признаками (показателями), полученными по результатам его объективного обследования:
- x1 — частота пульса,
- х2 – частота дыхания,
- x3 — среднее артериальное давление.
В этом случае состояние одного больного, описываемое точкой (вектором) X = (x1, x2,x3) в 3-мерном пространстве, должно быть отнесено к одному из двух классов: w1 или w2 (рис. 1).
Разделяющие поверхности в признаковом пространстве. Дискриминантные функции
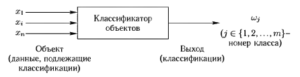
Таким образом, классификатор объектов является устройством, которое отображает точки из Еn в множество классов {w1,w2,…,wm} (рис. 2). Обозначим через Ri, множество точек из Еn, которое отображается в класс wi.
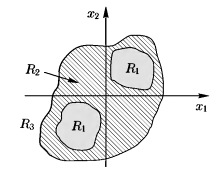
Тогда множеству классов {w1,w2,…,wm} будет соответствовать множество областей из Еn {R1,R2,…,Rm}. Например, на рис. 3, где n = 2, m = 3, любая точка на плоскости в зависимости от ее принадлежности к областям R1,R2,R3 отображается, соответственно, в один из классов w1,w2,w3, Все три области отделены друг от друга поверхностями (кривыми в Е2), которые мы будем называть разделяющими.
Разделяющие поверхности любого классификатора объектов можно полностью определить m скалярными функциями: D1(X), …,Dm(Х), называемыми дискриминантными функциями (ДФ). Они выбираются так, чтобы для всех Х ∈ Ri, выполнялось Di(Х) > Dj(X) при i, j = 1, …, m; i ≠ j. Мы также предполагаем, что ДФ непрерывны на разделяющих поверхностях. Тогда поверхность, разделяющая смежные области Ri и Rj, определяется уравнением
Di(X)-Dj(X) = 0. (1.1)
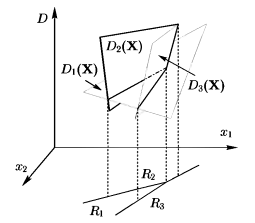
На рис. 4 показаны три ДФ и области решений, порождаемые ими на плоскости x1, x2.
Введение понятия дискриминантных функций преобразует модель классификатора объектов к виду рис. 5, где дискриминаторами названы блоки, вычисляющие дискриминантные функции.
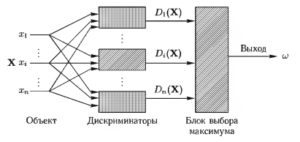
Данные функции могут принадлежать к разным видам (линейные, кусочно-линейные, нелинейные, квадратичные). При решении задач распознавания образов существует проблема выбора вида ДФ.
Линейные дискриминантные функции
К простейшим дискриминантным функциям относятся линейные (ЛДФ), определяемые выражением
![]()
Для i = 1 ЛДФ имеет вид
D1(X) = w11x1 + w12x2 + w13x3 + … + w1(n+1).
В этом случае поверхность, разделяющая смежные области Ri и Rj, в Еn определяется из (1.1)
![]() (1.2)
(1.2)
где wk = wik – wjk, wn+i = wi(n+1) – wj(n+1).
Полученное уравнение это уравнение гиперплоскости в пространстве Еn.
Если m = 2, то уравнение (1.2) превращается в следующее:
D(X) = D1(X) – D2(Х) = w1x2 + w2x2 +… + wnxn + wn+1 = 0,
и по знаку новой дискриминантной функции D(X) мы можем отнести входной объект к одному из двух классов — w1 или w2.
Если D(X) >0, то R1 и входной объект относится к классу w1.
Если D(X) < 0, то R2 и входной объект относится к классу w2.
Введя пороговый логический блок (ПЛБ), классификатор для этого случая можно изобразить, как показано на рис. 6.
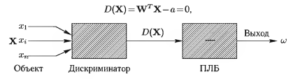
Вышеприведенное выражение для £)(Х) можно также записать в виде
D(X)=WTX—а=0,
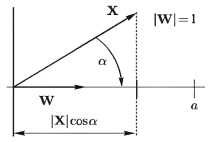
где W — весовой вектор; 0 — пороговая величина. Удобно сделать вектор W единичным, разделив все компоненты на норму этого вектора. В этом случае, так как WTX = |X|cos a (рис. 7), то процедура распознавания заключается в вычислении проекции вектора X на направление весового вектора W и сравнении полученной величины с порогом а. Также ясно, что разделяющая гиперплоскость проходит перпендикулярно к W на расстоянии а от начала координат.
Существует ряд методов определения W и а, основанных как на критериях теории статистических решений, так и на максимизации определенного некоторым образом расстояния между классами.
Классификатор ЭЭГ
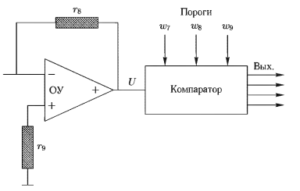
Примером линейного классификатора является классификатор электроэнцефалограмм (ЭЭГ) (рис. 8). На вход устройства подается сигнал ЭЭГ, обозначенный как z(t). В устройстве вычисляется 6 признаков (параметров):
- x1 — число пересечений нулевой линии,
- x2 — средняя амплитуда исходной ЭЭГ,
- x3 — число максимумов и минимумов,
- x4 — средняя амплитуда 1-й производной,
- x5 — число точек перегиба,
- x6 — средняя амплитуда 2-й производной.
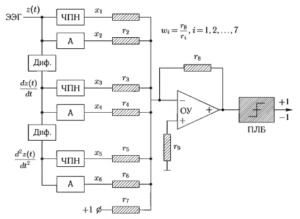
Как видно из рисунка, сигнал U на выходе ОУ равен
![]()
гдe ![]()
В случае, когда некоторые wi отрицательны, в схеме перед соответствующими ri необходимо поставить инверторы. Сигнал на выходе ПЛБ равен +1, если U > 0, и —1, если U < 0.
Реальная схема классификатора немного сложнее. Она разбивает не на 2, а на 4 класса за счет использования не одного, а 3 порогов. В этом случае на рисунке соединение с r7 удаляется, а правая часть рисунка приобретает вид рис. 9. Сравнение с порогами производится по следующему правилу:
если ![]() тo ЭЭГ относится к классу 1, иначе
тo ЭЭГ относится к классу 1, иначе
если ![]() то ЭЭГ относится к классу 2, иначе
то ЭЭГ относится к классу 2, иначе
если ![]() , то ЭЭГ относится к классу 3, иначе
, то ЭЭГ относится к классу 3, иначе
если ![]() , то ЭЭГ относится к классу 4 .
, то ЭЭГ относится к классу 4 .
Данный классификатор используется для определения глубины наркоза, стадий сна, изучения биологических обратных связей, влияния лекарственных препаратов на ЭЭГ и других целей.
Классификатор по минимуму расстояния
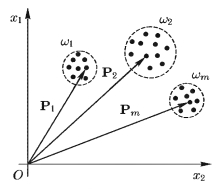
Пусть в n-мерном признаковом пространстве мы имеем m эталонных векторов P1, Р2, …. Рm, каждый из которых является эталоном (шаблоном) своего класса (эталонных векторов), как изображено на рис. 10. Вектор Рi = (рi1, рi2…..pin) соответствует классу wi. Классификатор по минимуму расстояния относит входной вектор X к том классу wi, для которого расстояние |Х – Pi| между X и эталонным вектором Pi минимально. Вместо расстояния |Х – Pi| можно взять его квадрат |Х – Pi|2. Так как |Х – Pi| = √(Х – Pi)Т(Х – Pi), то |Х – Pi|2 = (X – Рi)Т(Х – Рi) и на основании свойства дистрибутивности скалярных произведений векторов имеем
|Х – Рi|2 = ХТХ – XTPi – РiTХ + РiTРi. (1.3)
Произведение XTX = |Х| на расстояние не влияет, а на основании свойства коммутативности скалярных произведений векторов справедливо равенство XTРi = РiTX. так как
![]()
Тогда, исключив XTX из выражения (1.3), поменяв знаки и поделив все члены на 2, получим дискриминантную функцию Di(X) для класса Она имеет вид
Di(Х) = ХТРi -½РiТPi; i = 1, …, m. (1.4)
Как и ранее, входной вектор X относится к классу wi. если
Di(Х) > Dj(Х), i, j=1…..m, i ≠ j.
Выражение (1.4) также можно написать в виде
Di(X) = x1wi1 + x2wi2 +… + xnwin + wi(n+1), i = 1, …, m,
где wij=pij i=1, …, m, j=1,…,n;
wi(n+1) = -½(p2i1 +p2i2 + … +p2in) , i=1, …, m
Таким образом, видно, что классификатор по минимуму расстояния является линейным классификатором. Такой классификатор целесообразно применять в случаях, когда каждый класс имеет свой эталонный объект Рi, вокруг которого группируются остальные объекты этого класса.
При m = 2 (два класса)
D1(Х) = ХТР1 – ½ Р1TР1 , D2(Х) = ХТР2 – ½ Р2TP2.
D0(X) = D1(X) – D2(X) = XTР1 – XTP2 – ½ (Р1TР1 – Р2TP2).
Добавим к выражению в скобках член Р1TР2 и вычтем равный ему Р2TР1. Тогда
D0(Х) = ХТ(Р1 – Р2) – ½ (Р1TР1 – Р1TР2 +Р2TР1 – P2TP2).
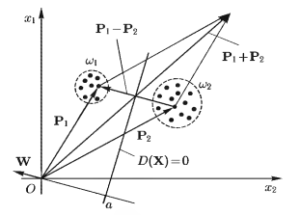
D0(X) = ХТ(Р1 – P2) – ½(Р1 + P2)T(Р1 – P2).
Разделим все члены последнего выражения на |Р1 — Р2|. Тогда
![]()
![]()
Нa рис. 1.11 показана разделяющая (линейная) граница D(Х) =0 между двумя классами, проведённая для классификации по минимуму расстояния до эталонов классов.
Footnotes
- Ту Дж., Гонсалес Р. Принципы распознавания образов / Пер. с англ.; Пол ред. Ю. И. Журавлева. М.: Мир, 1978. — 411 с.
- Дуда 3., Харт П. Распознавание образов и анализ сцен / Пер. с англ. — М.: Мир, 1976. – 511 с.
- Вапник В. //., Червоненкис Л. Я. Теория распознавания образов. Стохастические проблемы обучения. — М.: Наука, 1974.
- Нильсон Н. Обучающиеся машины / Пер. с англ. — М.: Мир, 1967. -180 с.
- Фу К. Структурные методы в распознавании образов / Пер. с англ. -М.. Мир, 1977. – 320 с.
- Рангайян Р. М. Анализ биомедицинских сигналов. Практический подход / Пер. с англ. А. II. Калиниченко; Под ред. Л. П. Немирно. -М.: Физматлит, 2007. — 440 с.
- Гублер Е. В. Вычислительные методы анализа и распознавания патологических процессов. Л.: Медицина, 1978. 290 с.
- Генкин А. А., Медведев В. И. Прогнозирование психофизиологических состояний. Вопросы методологии и алгоритмизации. — Л.: Наука. 1973. — 144 с.
- Рангайян Р. М. Анализ биомедицинских сигналов. Практический подход / Пер. с англ. А. II. Калиниченко; Под ред. Л. П. Немирно. -М.: Физматлит, 2007. — 440 с.
- Немирно А. П. Цифровая обработка биологических сигналов. М.: Наука, 1984. — 144 с.