Идентификация сложных биосигналов с использованием оценок условной энтропии
Ряд задач анализа биомедицинских сигналов заключается в распознавании фрагментов конечной длины по степени выраженности детерминированных и случайных компонентов, обнаружении нерегулярных дискретных последовательностей. Эго может быть анализ вариабельности сердечного ритма в различных состояниях живого организма, распознавание приступов мерцательной аритмии и т.п. Одним из методов их решения является подход, основанный на теории информации Э. Шеннона1.
Под регулярностью временного ряда, преобразованного посредством квантования и символьного кодирования в последовательность состояний, понимается статистическая устойчивость структуры переходов, наблюдаемая во времени. В качестве индикатора появления новых последовательностей, нс согласованных с предшествующими, предлагается использовать условную энтропию234. Анализ изменения этого показателя во времени, т.е. при удлинении цепочек символов, может служить эффективной мерой нерегулярности временного ряда.
Вычисление и выбор параметров условной энтропии
Вычисление условной энтропии предполагает выполнение определенной последовательности шагов. Вначале для заданной выборки x(i), i= 1,2…..N формируется ряд L-мерных последовательностей {XL(i), i = 1,2…..(N – L + 1)}. XL(i) = (х(i), ,x(i+ I), …, x(i + L – 1)). Затем посредством операции квантования и последующего преобразования из числовой в символьную форму это множество задается в виде множества последовательностей состояний {ZL(i),i = 1,2, …, (N – L + 1)}. При этом каждый элемент последовательности ZL(i) = (z(i), z(i + 1)…..z(i + L – 1)) кодируется символами из произвольного алфавита А = {аР}, р= 1, …,ξ. результате такого преобразования получаем упорядоченные по i последовательности событий, связанных с интервальной оценкой каждого отсчета x(i) в диапазоне (xmin, xmax)- Они рассматриваются далее как цепочки символов длины L. Изменяя параметр L, можно сформировать последовательности событий разной длины и перейти к вычислению условной энтропии.
Известно5, что условная энтропия определяется в виде
![]() (2.4)
(2.4)
где PL/L-1 — вероятность появления конкретного символа в последней, L-й ячейке цепочки длины L при условии выделения всех одинаковых цепочек укороченной длины L-1; PL-1 — вероятность появления конкретной цепочки событий длины L — I.
Величина E(L/L – 1) определяет дополнительную информацию, необходимую для предсказания L-го события в любой последовательности {ZL(i)}, i = 1,2, (N – L + 1). если известна вся последова тельность предыдущих событий. Она может быть вычислена еще и как приращение, получаемое безусловной энтропией E(L) при переходе от последовательности событий длины (L – I) к длине L:
![]() (2.5)
(2.5)
Для выборок большой длины (N → ∞) значение E(L/L – 1) при увеличении L стремится к нулю для регулярных процессов и к постоянному положительному значению для процессов с чисто случайными свойствами. Однако при анализе конечной выборки отсчетов замена вероятностей в (2.3) и (2.4) значениями частот попадания x(i) в соответствующие интервалы приводит к значительному смещению оценки E(L/L — 1). Известно, что для последовательности событий длиной L значение E(L) ограничено сверху значением log(N – L + 1). и поэтому E(L/L – 1) с ростом L будет стремиться к нулю независимо от вида анализируемого процесса. Это приводит к тому, что даже для чисто случайного процесса может быть обнаружена ложная регулярность.
В процессе обработки значения x(i) квантуются по ξ интервалам и для {ZL-1(i)} пространство состояний оказывается разделенным на ξL—1 областей. Каждая из них является возможным местоположением любой цепочки указанной длины. С увеличением L количество ячеек экспоненциально возрастает, вследствие чего увеличивается и число областей, содержащих лишь одну последовательность событий. При добавлении L-го элемента к таким цепочкам длины (L — 1) получаем нулевой вклад в вычисляемое приращение энтропии и в результате оценки E(L/L – I) редкие события идентифицируются как детерминированные. Па самом деле такие цепочки являются «неизвестными» в смысле предсказуемости динамики поведения на последующих интервалах (L, L + 1, L + 2, …). Для исключения ложной регулярности, вносимой в оценку условной энтропии одиночными цепочками, могут применяться следующие виды коррекции:
E1(L/L- 1) = E(L/L – 1)(1 + NL-1(1)/(NL – NL-1(1)). (2.6)
E2(L/L- 1) = E(L/L – 1) + E(1)NL-1(1)/(NL) (2.7)
где NL — число анализируемых цепочек символов длиной L, NL-1(1) число одиночных цепочек символов длиной (L – 1).
В выражении (2.5) одиночным цепочкам придается среднее приращение энтропии, оцениваемое по (NL – NL-1(1)) — числу последовательностей событий. В формуле (2.6) таким событиям присваиваются веса Е(1), соответствующие энтропии одиночных событий. Благодаря этому «неизвестные» цепочки рассматриваются как случайные, а не как регулярные последовательности. Это позволяет избежать ложного представления о не подтвержденных регулярных изменениях в исследуемых последовательностях. Введение весов, задаваемых величиной Е(1), было обосновано в работе6, однако придавались они всем одиночным событиям, обнаруженным на L-м шаге, что приводило к значительному смещению энтропии. В работах78 в разряд совершенно случайных событий переводятся лишь те цепочки, которые были представлены лишь одним объектом в ячейках (L-1)-мерного пространства состояний.
На рис. 1 представлены зависимости оценок условной энтропии от длины цепочек L для трех видов модельных сигналов: а — гармонического сигнала, б — шума, в — аддитивной смеси сигнала и шума. Из анализа кривых следует, что для гармонического сигнала их изменения практически совпадают, а при наличии шума — существенно различаются.
Эти различия связаны с коррекцией условной энтропии лишь по числу одиночных цепочек, равному NL-1(1). При этом оценка E1(L/L — 1) незначительно уменьшает крутизну изменения условной энтропии, а оценка E2(L/L— 1) приближается к постоянному уровню, задаваемому величиной E(1), что можно интерпретировать как искусственное «зашумление» анализируемого сигнала. На рис. 1, г приведены зависимости величины NL(1) от длины L для гармонического сигнала (кривая а), шума (б) и смеси гармонического сигнала и шума (в). Из рисунка видно, что для выборки ограниченной длины N с увеличением L быстро растет число «неизвестных» цепочек при наличии в сигнале случайной составляющей, что и требует введения коррекции функции E(L/L- I).
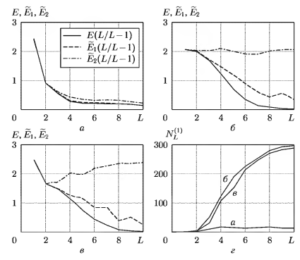
На основе анализа полученных зависимостей выбраны следующие параметры для идентификации сигналов. Во-первых, это могут быть точечные оценки скорректированной кривой E1(L/L 1) или E2(L/L – I) при значениях L = 2, 3, 4, т.е. в той области, где вклад одиночных цепочек незначителен. Это позволяет в дальнейшем использовать их в качестве дискриминантных признаков при решении задач классификации. Во-вторых, в качестве меры нерегулярности процесса может быть использована нижняя граница кривой E2(L/L — 1), которая принимает малое значение для регулярных процессов и большое в случае наличия выраженных случайных изменений. В работах910 с этой целью вычислялся относительный минимум ME, задаваемый в виде: МЕ=Е(1) — min {E2(L/L — 1)}. Чем выше регулярность процесса, тем больше значение показателя ME. Эксперименты на реальных данных позволили установить, что функция E2(L/L — 1) и показатель ME могут использоваться для оценки степени регулярности изменений, наблюдаемых во временных рядах конечной длины, а также могут найти применение в задаче распознавания нарушений ритма со сложной динамикой распределения кардиоинтервалов.
Распознавание фрагментов мерцательной аритмии
Оценка ME была использована при анализе нарушений ритма сердца, в частности, в задаче распознавания мерцательной аритмии по последовательности кардиоциклов длиной N = 3001112. В процессе исследования было обработано более 150 записей ЭКГ, для которых были построены ритмограммы и вычислен относительный минимум функции E2(L/L — 1). Анализ результатов эксперимента показал, что параметр ME имеет устойчивые интервальные оценки при уровне значимости о = 0,05 для разных видов рассматриваемых ритмограмм, причем значение этого параметра при мерцательной аритмии значительно меньше. Так, для нормального ритма с волновой структурой ритмограммы значение А/Е равно (0,85 ±0,09). При частой желудочковой экстрасистолии, для которой характерны кратковременные регулярные изменения в последовательности RR-интервалов, оно несколько меньше (0,74 ±0,10). И только при мерцательной аритмии, отличающейся нерегулярным распределением длительностей кардиоциклов, показатель ME значительно меньше (0,17 ±0,11).
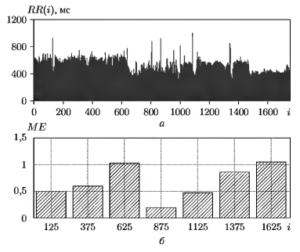
На рис. 2 в качестве примера показан результат динамического анализа параметра А/Е для сложной последовательности RR-интервалов, содержащей кратковременный приступ мерцательной аритмии. При попадании текущего окна обработки длиной N = 250 на область данных, содержащих хаотические изменения ритмограммы, значение ME резко уменьшается, что является индикатором появления приступа аритмии. В ходе многочисленных модельных и реальных экспериментов установлено, что показатель MЕ, являющийся интегральным параметром скорректированной условной энтропии, может эффективно использоваться для идентификации нерегулярных последовательностей, в частности, для распознавании фрагментов мерцательной аритмии в ходе автоматического слежения за ЭКГ больного.
Footnotes
- Шеннон К. Работы по теории информации и кибернетике / Пер. с англ. —М., 1965. 438 с.
- Манило Л. А. Идентификация биосигналов методами оценки условной энтропии // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. 2005. Вып. 2. С. 53-59.
- Manilo L. A. Detection of biocological signals with chaotic properties through assessment of conventional entropy / 9-th Intern, conf. «Pattern recognition and image analysis: new information technologies» (PR IA-9-2008), Nizhni Novgorod // Conf. proc. 2008 Vol. 2. P. 11-14.
- Porta I., BaselIi G., Liberal/ D. et al. Measuring regularity by means of a corrected conditional entropy in sympathetic outflow // Biological Cybernetics. 1998. Vol. 78. P. 71-78.
- Шеннон К. Работы по теории информации и кибернетике / Пер. с англ. —М., 1965. 438 с.
- Porta I., BaselIi G., Liberal/ D. et al. Measuring regularity by means of a corrected conditional entropy in sympathetic outflow // Biological Cybernetics. 1998. Vol. 78. P. 71-78.
- Шеннон К. Работы по теории информации и кибернетике / Пер. с англ. —М., 1965. 438 с.
- Manilo L. A. Detection of biocological signals with chaotic properties through assessment of conventional entropy / 9-th Intern, conf. «Pattern recognition and image analysis: new information technologies» (PR IA-9-2008), Nizhni Novgorod // Conf. proc. 2008 Vol. 2. P. 11-14.
- Манило Л. А. Идентификация биосигналов методами оценки условной энтропии // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. 2005. Вып. 2. С. 53-59.
- Manilo L. A. Detection of biocological signals with chaotic properties through assessment of conventional entropy / 9-th Intern, conf. «Pattern recognition and image analysis: new information technologies» (PR IA-9-2008), Nizhni Novgorod // Conf. proc. 2008 Vol. 2. P. 11-14.
- Манило Л. А. Идентификация биосигналов методами оценки условной энтропии // Изв. СПбГЭТУ «ЛЭТИ». Сер. Биотехнические системы в медицине и экологии. 2005. Вып. 2. С. 53-59.
- Манило Л. А. Распознавание фибрилляции предсердий в кардиологических системах диагностики и наблюдения // Биотехносфера. 2009, № 2. С. 41 45.