Рассмотренные ранее энтропийные характеристики применялись также для анализа свойств ЭЭГ-сигнала в разных стадиях анестезии12 и распознавания стадии глубокого наркоза34. В работе5 для оценки глубины наркоза по ЭЭГ предложено использовать показатель аппроксимированной энтропии АрЕn(2).
Известно, что изменение уровня функциональной активности головного мозга вызывает характерные изменения, наблюдаемые в ЭЭГ-сигнале6. Высокий уровень активности мозга сопровождается сложным ЭЭГ-сигналом, имеющим хаотический вид. Снижение степени функциональной активности отражается на ЭЭГ появлением регулярных низкочастотных колебаний достаточно большой амплитуды. В разных стадиях анестезии выраженность регулярных и хаотических изменений ЭЭГ-сигнала различна.
На рис. 1 приведены четыре фрагмента ЭЭГ-сигнала, зарегистрированного на одном пациенте в разных стадиях проводимой анестезии: до начала анестезии («), в начальной стадии (б) и при выходе из анестезии (в), в стадии окончательного пробуждения (г). Частота дискретизации ЭЭГ-сигнала составляет 500 Гц, длительность фрагментов — 10 с. Для этих сигналов рассчитаны рассмотренные энтропийные характеристики, причем длительность анализируемых фрагментов выбрана равной 5 с.
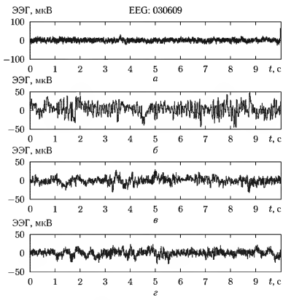
а — до начала анестезии, б — глубокий наркоз, в — выход из анестезии, г — окончательное пробуждение
Рисунок 2 иллюстрирует результат вычисления аппроксимированной энтропии для двух последовательных 5-секундных фрагментов ЭЭГ при значении r= 0,2σх. Как видно из рисунков, в начальной области изменения параметра m кривые имеют явные отличия при разных функциональных состояниях головного мозга.
Выбор параметра АрЕn(2) для оценки уровня анестезии обусловлен тем, что при увеличении m возрастает число одиночных последовательностей и из-за их нулевого вклада в оцениваемые показатели энтропии возникает эффект ложной регулярности сигнала. При выбранном значении m = 2 надежность показателя энтропии значительно выше. Как следует из численного анализа АрЕn(2), оцениваемые параметры более чем в 2 раза уменьшают свои значения при переходе от активного состояния к стадии глубокого наркоза. Кроме того, выход из наркоза и переход к окончательному пробуждению сопровождается постепенным возрастанием значений АрЕn(2).
Для приведения показателя энтропии к принятой в анестезиологии шкале (0…100) использована нормировка по значению абсолютной энтропии АрЕn(0). В этом случае следует ожидать значений энтропни, близких к 100, для сигнала ЭЭГ, зарегистрированного до начала анестезии и в стадии полного пробуждения. При глубоком наркозе, очевидно, показатель АрЕn(2) будет иметь довольно малые значения.
На рис. 3 приведены результаты вычисления нормированного показателя АрЕn(2) /АрЕn(0) для выборки ЭЭГ-сигналов (64 реализации длиной 5 с каждая), зарегистрированных у восьми пациентов в клинических условиях во время проведения операции. Они представлены в графическом виде как разброс точек на вертикальных линиях с координатами: 1 — до начала анестезии, 2 — глубокий наркоз. 3 — выход из наркоза, 4 — окончательное пробуждение. Каждая точка — это результат вычисления энтропийного показателя для одной 5-секундной реализации ЭЭГ. Как видно из рисунка, на линиях 1 и 2 образованы непересекающиеся множества объектов. Очевидно, что при пороговом значении аппроксимированной энтропии на уровне 0,45 можно для исследуемой выборки данных решить задачу распознавания стадии глубокого наркоза. Стадии 3 и 4 образуют группы точек, занимающие промежуточное между состояниями 1 и 2 положение, что соответствует существующему представлению о процессе выхода из наркоза.
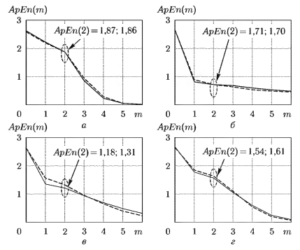
а — до начала анестезии; б — глубокий наркоз; в — выход из наркоза; г — пробуждение
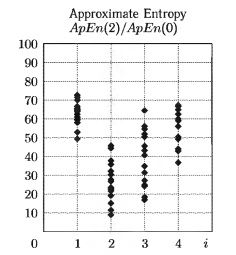
В качестве показателя эффективности применения АрЕn(2) /АрЕn(0) для распознавания стадии наркоза выбран критерий Фишера J. Он вычислялся по множествам значений параметра энтропии для двух следующих друг за другом состояний (1 → 2; 2 → 3; 3 → 4). Всего в ходе эксперимента проанализированы электроэнцефалограммы 31 пациента. В результате обработки 124 реализаций ЭЭГ длительностью 10 с каждая получены следующие значения: J1,2 = 3,07; J2,3 = 0,78; J3.4 =0.47. Оценка энтропийных параметров проводилась по коротким 5-секундным фрагментам ЭЭГ-сигнала.
Как следует из анализа значений критерия J, а также данных, приведенных на рис. 3, метод оценки параметра АрЕn(2) позволяет решить задачу распознавания двух состояний: бодрствование и глубокий наркоз. Это дает основу для дальнейшего исследования энтропийного подхода при распознавании промежуточных стадий анестезии.
Оценка глубины наркоза по ЭЭГ на основе спектральной энтропии
Контроль глубины анестезии в ходе проведения хирургических операций является важнейшей задачей врача-анестезиолога. При этом важно поддерживать необходимую глубину наркоза и не допускать передозировки анестетиков. Результаты многочисленных исследований789 показывают, что одним из наиболее информативных методов инструментального контроля глубины анестезии может служить автоматический анализ электроэнцефалограммы (ЭЭГ) пациента. При переходе пациента из состояния бодрствования в состояние глубокого наркоза в его ЭЭГ наблюдаются характерные изменения, проявляющиеся как в спектральных характеристиках сигнала, так и в степени его хаотичности. Поэтому наиболее часто для автоматического анализа глубины анестезии по ЭЭГ предлагаются следующие два подхода: анализ частотных свойств сигнала10 и оценка энтропийных показателей1112.
Существуют различные способы вычисления энтропии сигнала. Во временной области рассматривают, например, аппроксимированную энтропию или энтропию Шеннона. В частотной области может быть рассчитана спектральная энтропия (СЭ), важным преимуществом которой является то, что вклад в энтропию составляющих, лежащих в любом заданном диапазоне частот, может быть выделен отдельно.
Основой для расчета СЭ является оценка спектральной плотности мощности сигнала (СПМ). Наиболее часто для получения оценки СИЛА сигнала используется дискретное преобразование Фурье, позволяющее получить из последовательности отсчетов равномерно дискретизованного с частотой fд сигнала x(n) = x(nТ), где Т = 1/fд -интервал дискретизации, такое же количество комплексных величин Хк 13
![]() ,
,
где N — число отсчетов в анализируемом фрагменте сигнала, а каждый из элементов преобразования X(k) соответствует частоте f(k) = = kfд/N.
Вычисление СЭ основано на энтропии Шеннона14. При этом эта характеристика применяется не к самому сигналу, а к его спектру. СЭ в некотором диапазоне частот [f1,f2] для заданного фрагмента сигнала может быть вычислена при помощи следующей последовательности шагов.
Путем возведения в квадрат амплитуды каждого из элементов X(k) преобразования Фурье от сигнала x(n) рассчитывается соответствующее значение спектра мощности Р(к):
Р(k) = Х(k)X*(k),
где X*(k) представляет собой комплексно сопряженное значение элемента разложения Фурье Х(k).
Далее спектр мощности нормализуется, для чего рассчитывается такая константа нормализации Сн, что сумма нормализованного спектра мощности в пределах заданного диапазона частот [f1,f2] равняется единице. Тогда значения нормализованного спектра мощности Рн(k) рассчитываются как
![]()
Спектральная энтропия, соответствующая диапазону частот [f1,f2], рассчитывается как сумма:
![]()
После этого вычисляется нормализованный по диапазону от 0 (полная регулярность) до КХ) (максимальная нерегулярность) показатель спектральной энтропии ЕН[f1,f2]. для чего рассчитанное ранее значение Е[f1,f2]] делится па коэффициент log(N[f1,f2]), где N[f1,f2] равно общему числу частотных компонентов в диапазоне [f1,f2]:
![]()
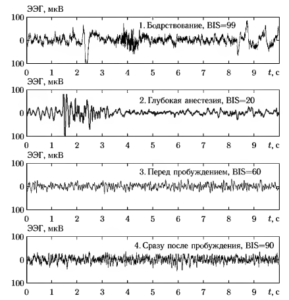
На рис. 4 приведены примеры сигналов ЭЭГ одного и того же пациента для четырех различных стадий общей анестезии: а) бодрствование непосредственно перед началом анестезии (состояние 1); б) — глубокий наркоз, достигаемый через несколько минут после начала анестезии (состояние 2); в) — этап хирургической операции через 1-2 часа после начала анестезии, когда состояние наркоза поддерживается за счет периодического введения дополнительных доз анестезирующих препаратов (состояние 3); г) — момент времени сразу после пробуждения пациента (состояние 4).
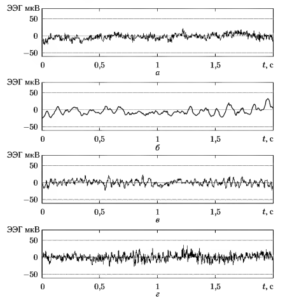
а) — состояние 1; б) — состояние 2; в) - состояние 3; г) состояние 4
a) — состояние I; б) — состояние 2; б) —состояние 3; г) — состояние 4
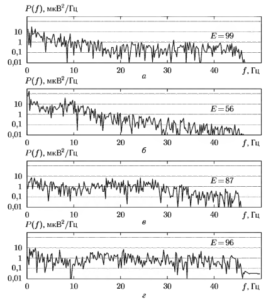
На рис. 5 приведены графики СИМ (в логарифмическом масштабе), рассчитанной с использованием алгоритма БПФ для тех же фрагментов ЭЭГ. Как по самим сигналам ЭЭГ, так и по графикам СИМ хорошо заметно, что в состоянии глубокого наркоза преобладают частоты в диапазоне от 0 до 30 Гц, что соответствует типичному частотному диапазону ЭЭГ. В состоянии бодрствования можно отметить существенное возрастание вклада более высокочастотных составляющих, что объясняется наличием миографической активности. Также на графиках СИМ приведены значения показателя СЭ, рассчитанные для диапазона частот от 1 до 47 Гц. Можно отметить, что в состояниях 1 и 4, соответствующих бодрствованию пациента, показатель СЭ имеет более высокие значения, чем в состояниях 2 и 3, соответствующих различным стадиям анестезии.
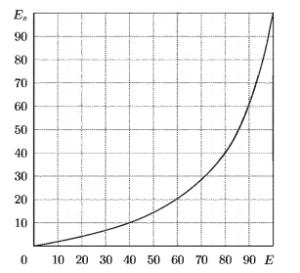
Для повышения информативности показателя спектральной энтропии в областях значений, соответствующих глубокому наркозу и переходу к состоянию бодрствования, необходимо использовать дополнительное преобразование с использованием нелинейной шкалы, эмпирически выведенное выражение для которой имеет вид:
Es=2400/(120- Е) – 20
где Е и Es — соответственно значения спектральной энтропии до и после применения нелинейной шкалы. На рис.6 приведен график данной шкалы.
В таблице 1 приведены вычисленные значения СЭ и значения, полученные в результате применения нелинейной шкалы. Можно видеть, что в последнем случае достигается гораздо более отчетливая дифференциация различных состояний пациента.
Таблица 1
| Состояние пациента | Вычисленное значение СЭ, Е | Значение СЭ Еs, полученное с помощью нелинейной шкалы |
| 1 | 99 | 94 |
| 2 | 56 | 18 |
| 3 | 87 | 53 |
| 4 | 96 | 80 |
Исследования, проведенные с использованием объемной выборки реальных записей ЭЭГ, зарегистрированных в ходе хирургических операций, показали, что показатель глубины анестезии, рассчитанный на основе одной только спектральной энтропии, хоть и позволяет с достаточно высокой точностью различать состояния бодрствования и наркоза, но в то же время не всегда дает возможность надежной дифференциации различных стадий анестезии1516. В связи с этим возникает необходимость анализа дополнительных количественных показателей глубины анестезии, которые могут быть рассчитаны по сигналу ЭЭГ. Ниже представлены результаты исследования1718, направленного на создание практического алгоритма, использующего комбинацию альтернативных признаков, характеризующих различные проявления в сигнале, связанные с применением общей анестезии.
Для проведения данного исследования был сформирован набор верифицированных записей ЭЭГ, полученных в ходе хирургических операций. Набор содержал 54 записи сигнала ЭЭГ общей продолжительностью более 140 часов. Использовалась частота дискретизации 500 Гц и разрядность 24 бита. Для верификации записи с точки зрения оценки глубины анестезии использовались поминутно регистрировавшиеся показания контрольного прибора (монитора анестезии BIS А-2000ХР, Aspect Medical), подключенного к тому же пациенту с использованием отдельного комплекта электродов. В качестве показателя использовался выдаваемый прибором на индикацию так называемый BIS-индекс19. принимающий значения в диапазоне от 0 до 100.
Исследование проводилось с использованием специально подготовленной выборки фрагментов сигнала, взятых из описанного выше набора. Выборка включала 23 группы по 4 фрагмента. Длительность каждого фрагмента — 60 с. Фрагменты каждой группы выбирались из одной записи ЭЭГ. Четыре фрагмента в группе соответствовали четырем различным состояниям пациента, характерным для применения общей анестезии и описанным в табл. 2.
На рис. 7. Показаны четыре десятисекундных фрагмента, взятых из одной и той же группы записей и соответствующих четырем описанным в табл. 2 состояниям пациента.
Переход от одной стадии анестезии к другой сопровождается изменениями в частотном составе ЭЭГ. Для использования этого свойства на практике необходимо получить некоторые количественные оценки этих изменений. Для экспериментальных исследований использовались фрагменты ЭЭГ. соответствующие двум следующим стадиям анестезии:
- глубокий наркоз, достигаемый через несколько минут после начала анестезии (состояние 2, B1S = 20);
- этап хирургической операции через 1-2 часа после начала анестезии (состояние 3, BIS = 60)-
Таблица 2. Критерии выбора фрагментов ЭЭГ
| Условный номер состояния | Стадия операции | Состояние пациента | Значение BIS-индекса |
| 1 | Перед применением анестезии | Бодрствование до применения анестезии | 95 100 |
| 2 | Через несколько минут после применения первой дозы анестетика | Глубокая анестезия | 15-25 |
| 3 | Через 1-2 часа после первого применения анестезии | Стабильное состояние анестезии | 55 65 |
| 4 | Пробуждение после окончания операции | Бодрствование сразу после выхода из состояния анестезии | 85 95 |
Рассчитывался следующий показатель:
![]()
где Plow суммарная мощность в диапазоне частот f1 ≤ f ≤ f2 и Phigh — суммарная мощность в верхней части диапазона частот f3 ≤ f ≤ f4
Оценки спектральной плотности мощности (СИМ) рассчитывались с использованием метода Уэлча20, суть которою заключается в усреднении оценок СИМ, полученных для некоторого числа перекрывающихся сегментов записи сигнала. Перед использованием преобразования Фурье для каждого сегмента выполнялась операция удаления линейного тренда.
Таким образом, исследовались следующие параметры данной процедуры:
- f1,f2,f3, f4 — пределы выбираемых частотных диапазонов;
- Tfr, — суммарная длительность фрагмента сигнала для вычисления СПМ;
- tw— длительность сегмента сигнала (окна) для расчета БПФ;
- ΔТ — шаг сдвига окна по времени.
В качестве количественной оценки различия между некоторой исследуемой парой показателей «1» и «2» использовался следующий критерий, известный из теории линейного дискриминантного анализа21|:
![]()
где m1, m2 — средние значения рассчитанных показателей и s12, s22 — соответствующие значения дисперсий. Чем выше разделяющая способность анализируемого показателя, тем более высокие значения критерия J1,2 должны получаться.
В случае исследования двух состояний анестезин «2» и «3» оптимизация параметров процедуры вычисления показателя RР выполнялась с использованием описанного выше критерия, обозначаемого здесь J2,3 . Оптимизация выполнялась с использованием метода наискорейшего и спуска22. В результате был выбран следующий набор параметров: f1= 0 Гц, f2 = 0,8 Гц, f3 = 7 Гц, f4 = 16 Гц, Tfr = 30 с (15000 отсчетов сигнала при частоте дискретизации fд = 500 Гц). Tw = 8,192 с (4096 отсчетов), ΔТ = 1 с (500 отсчетов). Максимальная достигнутая величина критерия оптимизации при этом составила J2.3 = 3,46, что свидетельствует о достаточно хорошей разделяющей способности показателя
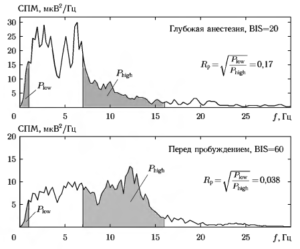
Пример графиков оценок СПМ для двух анализируемых состояний анестезии показан на рис. 8. Закрашенные области под кривой СПМ соответствуют значениям суммарной мощности, используемым для вычисления показателя RР. Как можно видеть, значения этого показателя, рассчитанные для двух различных состояний анестезии, существенно отличаются.
В состоянии глубокой анестезии в сигнале ЭЭГ часто наблюдается эффект, получивший название «вспышка-подавление» («burstsuppression»), который проявляется в чередовании сегментов сигнала с очень низкой амплитудой («подавление») и коротких высокоамплитудных всплесков сигнала («вспышка»). В качестве количественной оценки выраженности данного эффекта используют так называемое «отношение вспышка-подавление» («burst-suppression ratio»), вычисляемое как отношение суммарной продолжительности участков типа «подавление» TS к аналогичной величине для участков типа «вспышка» TB, подсчитанное за определенный промежуток времени:
RBS=TS/TB
Сегмент сигнала х(n), расположенный в промежутке между отсчетами, имеющими индексы n1 и n2, считается участком типа «подавление» в случае выполнения следующего условия:
|х(n)| < Хlim, n1 ≤n≤ n2,
где Хlim = ksx — пороговое значение, sх — стандартное отклонение анализируемого фрагмента сигнала, а k — эмпирически подобранный коэффициент. Процесс сегментации фрагмента ЭЭГ на участки типа «подавление» и «вспышка» иллюстрируется на рис. 9.
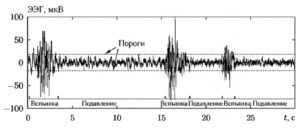
Исследовались следующие параметры процедуры сегментации:
- к — коэффициент, используемый для расчета Хlim;
- Тfr — общая продолжительность анализируемого фрагмента сигнала;
- Tw размер сегмента сигнала (окна) для расчета показателя RBS;
- ΔТ — шаг сдвига окна по времени.
В результате оптимизации был выбран следующий набор параметров: k= 0,8, Тfr= 40 с, (20000 отсчетов сигнала при частоте дискретизации fд 500 Гц), Tw = 5 с (2500 отсчетов), ΔТ =1 с (500 отсчетов). Достигнутая максимальная величина критерия J2.3 = 2,12 свидетельствует о наличии выраженной разделяющей способности отношения «вспышка-подавление»RBS.
Максимальные значения критерия достигнутые для оптимальных комбинаций параметров обоих рассмотренных выше методов, достаточно велики, чтобы продемонстрировать наличие некоторой разделяющей способности этих параметров с точки зрения дифференциации различных стадий анестезии, но в то же время не настолько высоки, чтобы обеспечить надежность и стабильность этой дифференциации.
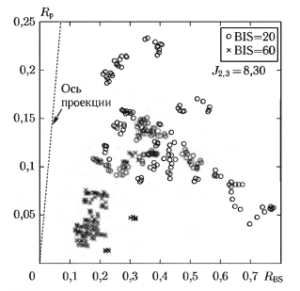
На рис. 10 представлено совместное распределение значений двух предложенных показателей RР и RBS . Для стадий анестезии, соответствующих значениям BIS-индекса 20 и 60. Это распределение, с одной стороны, демонстрирует отсутствие какой-либо корреляции между показателями, а с другой — показывает, что точки на плоскости, соответствующие двум различным состояниям, формируют практически изолированные области на плоскости. С использованием методов линейного дискриминантного анализа может быть найдено положение оптимальной оси проекции (пунктирная линия на графике), которая соответствует максимуму используемою критерия различимости состояний: J2.3 = 8.3. Проекции точек распределения на эту ось могут быть найдены с использованием выражения RBS,P =kBSRBS+kPRP , где kBS = 0,27 и kP = 0,96 — коэффициенты, определяющие положение оси проекции.
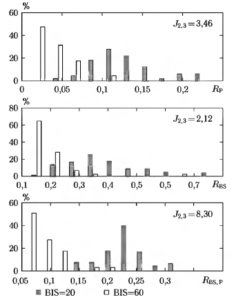
На рис. 11 приведены гистограммы распределения значений показателей RP, RBS и RBS,P. Можно отмстить, что значение критерия J2.3 = 8,3 для нижнего из распределений значительно выше, чем значения критериев, рассчитанных для каждого двух других случаев. Это означает, что комбинированное использование параметров RР и RBS позволяет получить достаточно хороший показатель глубины анестезии.
В результате проведения описанного исследования были получены два основных показателя глубины анестезии: оценка спектральной энтропии Es, обеспечивающая надежную дифференциацию между состояниями бодрствования и наркоза, и комбинированный показатель RBS,P. демонстрирующий способность к различению различных стадий анестезии. Была предложена следующая комбинация этих двух показателей:
![]()
![]()
где ![]() и
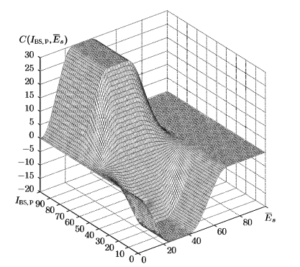
и ![]() — показатели Es и RBS,P, усредненные по пяти последним значениям, a C(IBS,P. Es) — экспериментально определенная поправка (см. график на рис. 12). Параметры предложенных правил получены в результате минимизации по методу наименьших квадратов расхождений между получаемыми значениями Е и соответствующими показаниями контрольного прибора.
— показатели Es и RBS,P, усредненные по пяти последним значениям, a C(IBS,P. Es) — экспериментально определенная поправка (см. график на рис. 12). Параметры предложенных правил получены в результате минимизации по методу наименьших квадратов расхождений между получаемыми значениями Е и соответствующими показаниями контрольного прибора.
На основе представленного здесь исследования был разработан практический алгоритм, реализованный в виде пакета программ на языке программирования С ++. Кроме описанных выше методов анализа ЭЭГ, практический вариант алгоритма включает также ряд процедур, повышающих его стабильность и устойчивость к шумам, в частности: текущий анализ уровня шумов, предварительная цифровая фильтрация, усреднение и медианная фильтрация рассчитываемых показателей, устранение изолированных всплесков в выходных значениях.
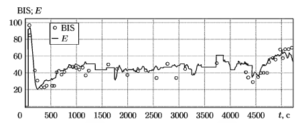
Для тестирования алгоритма был использован весь набор записей ЭЭГ, описанный выше (54 записи общей продолжительностью более 140 часов). Статистические параметры, характеризующие расхождения между рассчитанными значениями показателя Е и соответствующими показаниями контрольного прибора (BIS-монитора), представлены в табл. 3. На рис.13 показан пример сравнения показаний BIS-монитора (кружочки) и выходных значений тестируемого алгоритма (сплошная линия) для одной из записей ЭЭГ тестового набора.
Таблица 3. Результаты тестирования алгоритма
| Параметр | Максимум | Минимум | Среднее |
| Коэффициент корреляции | 0,91 | 0,67 | 0,78 |
| Стандартное отклонение. мкВ | 11,9 | 6,5 | 9,7 |
| Максимальная ошибка, мкВ | 33,2 | 15,6 | 23,1 |
Анализ результатов тестирования алгоритма показывает адекватность выходных показаний глубине анестезии. Большая часть выявленных ошибок была вызвана спонтанно возникающими скачкообразными изменениями выходных значений из-за высокого уровня помех во входном сигнале. Таким образом, дальнейшие усилия по совершенствованию алгоритма должны быть в основном направлены на повышение его устойчивости к помехам.
Footnotes
- Манило Л. А., Волкова С. С. Анализ параметров аппроксимированной энтропии в задаче оценки глубины наркоза по ЭЭГ // Биомедицинская радиоэлектроника. Биомедицинские технологии и радиоэлектроника. 2012, № I. С. 58- 61.
- Немирно А. П., Манило Л. А., Калиниченко А. Н., Волкова С. С. Сравнительный анализ применения различных оценок энтропии ЭЭГ-сигнала для распознавания стадий наркоза // БИОТЕХНОСФЕРА. 2010. Вып. 3. С. 3-10.
- Manilo L. A., Volkova S. S. Recognition of the deep anesthesia stage from parameters of the approximated entropy of EEG sigral // Pattern recognition and image analysis. 2013. Vol. 23, № I. P. 92-97.
- Использование показателей энтропии ЭЭГ-сигнала для распознавания стадий наркоза / А. П. Немирко, Л. А. Манило, А. Н. Калиниченко, С. С. Волкова // Интеллектуализация обработки информации: 8-я Между нар. конф. Респ. Кипр, г. Пафос, 17-24 окт. 2010 г.: сб. докл. — М.: МАКС Пресс, 2010. С. 454-457.
- Немирно А. П., Манило Л. А., Калиниченко А. Н., Волкова С. С. Энтропийные методы оценки уровня анестезии по ЭЭГ-сигналу // Информационно-управляющие системы. 2010, № 3. С. 69-74.
- Зенков Л. Р. Клиническая электроэнцефалография с элементами эпилептологии. — МЕДпрссс-Информ, 2004. — 367 с.
- Зенков Л. Р. Клиническая электроэнцефалография с элементами эпилептологии. Издательство: МЕДпресс-Информ, 2001. — 367 с.
- Hughes S., Griffiths R. Anaesthesia Monitoring Techniques // Anaesth. and Intensive Care Medicine. 2002. P. 477 480.
- Tong S., Thakor N. V. Quantitative F.F.G Analysis Methods and Clinical Applications. — Artech House. 2009. — 421 p.
- Kaul H. L., Bharti N. Monitoring Depth of Anaesthesia // Indian J. Anaesth. 2002. V. 46(4). P. 323-332.
- Bein В. Entropy / Best Practice & Research Clinical Anaesthesiology. 2006. V. 20, №. I P. 101-109.
- Bruhn J.2. et al. Shannon entropy applied to the measurement of the electroencephalographic effects of desflurane // Anesthesiology. 2001. V. 95. P. 30-35.
- Зенков Л. Р. Клиническая электроэнцефалография с элементами эпилептологии. Издательство: МЕДпресс-Информ, 2001. — 367 с.
- Bruhn J. et al. Shannon entropy applied to the measurement of the electroencephalographic effects of desflurane // Anesthesiology. 2001. V. 95. P. 30-35.
- Немирно А. П., Манило Л. А., Калиниченко А. // Волкова С. С. Сравнительный анализ применения различных оценок энтропии ЭЭГ-сигнала для распознавания стадий наркоза // БИОТЕХНОСФЕРА. 2010. Вып. 3. С. 3-10.
- Немирно А. П., Манило Л. А., Калиниченко А.Н., Волкова С. С. Энтропийные методы оценки уровня анестезии по ЭЭГ-сигналу // Информационно-управляющие системы. 2010, № 3. С. 69-74.
- Kalinichenko Л. N.. Manila L. A., Nemirko A. P. Analysis of Anesthesia Stages Based on the EEG Entropy Estimation // Pattern Recognition and Image Analysis. 2015. V. 25, № 4. P. 680 689.
- Kalinichenko A., Manito L.. Nemirko A. Recognition of Anesthesia Stages Based on Nonlinear EEG Analysis. Advances in Mass Data Analysis of Images and Signals in Medicine, Biotechnology, Chemistry, and Food Industry. Proceedings of the 9th International Conference, MDA 2014. St. Petersburg, Russia, July 2014, Petra Perner (Ed.). Ibai-publishing. P. 25-31.
- Tong S., Thakor N. V. Quantitative F.F.G Analysis Methods and Clinical Applications. — Artech House. 2009. — 421 p.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
- Дуда 3., Харт П. Распознавание образов и анализ сцен / Пер. с англ. — М.: Мир, 1976. – 511 с.
- Gill P. E., Murray W., Wright M. H. Practical Optimization. Academic. Press. 1981.- 401 p.