Метод линейного программирования

Построение линейных разделяющих функций с применением методов линейного программирования

Проблема нахождения разделяющей гиперплоскости, возникающая в задачах медицинской диагностики, в частности при обнаружении некоторых классов биомедицинских сигналов, может быть сформулирована и решена в виде задачи линейного программирования (ЛП)¹.

Определим распознаваемый объект как точку в m-мерном евклидовом пространстве признаков. Для множества объектов (j = 1,2, …) положение соответствующих точек задается вектором P_j = (p_1j,p_2j,…,p_mj), являющимся матрицей-столбцом. Предполагается, что для обучающей последовательности известна принадлежность объектов к одному из классов w₁ (j ∈ w₁) или w₂(j ∈ w₂).

Отнесение объекта P_j к одному из классов осуществляется в соответствии с правилом

$\left\{\begin{array}{ll}{\Lambda^{\mathrm{T}} \mathbf{P}_{j} \geqslant \theta,} & {j \in \omega_{1}} \\ {\Lambda^{\mathrm{T}} \mathbf{P}_{j}<\theta,} & {j \in \omega_{2}}\end{array}\right.$

(1.30) ,

где θ > 0, а вектор Λ = (λ₁, λ₂,…,λ_m) представлен в виде матрицы-строки.

Как видно из (1.30), по знаку линейной функции

Λ^TP_j – θ = λ₁p_1j+ λ₂p_2j + … + λ_mp_m_j – θ

можно судить о принадлежности объекта к одному из классов.

Геометрически это означает построение разделяющей гиперплоскости Λ^TP_j – θ = 0. Задачу нахождения элементов вектора Λ, удовлетворяющего системе линейных неравенств (1.30), можно решить с использованием методов ЛП.

Для этого рассмотрим задачу нахождения двух параллельных гиперплоскостей $\begin{aligned} \boldsymbol{\Lambda}^{\mathrm{T}} \mathbf{P} = \vec{\lambda}+\theta \end{aligned}$ и $\begin{aligned} \mathbf{\Lambda}^{\mathrm{T}} \mathbf{P} =-\underline{\lambda}+\theta \end{aligned}$ , для которых выполняются следующие условия:

$\begin{aligned} \boldsymbol{\Lambda}^{\mathrm{T}} \mathbf{P}_{j} & \geqslant \vec{\lambda}+\theta, \quad j \in \omega_{1} \end{aligned}$ (1.31)

$\begin{aligned} \mathbf{\Lambda}^{\mathrm{T}} \mathbf{P}_{j} \leqslant-\underline{\lambda}+\theta, & j \in \omega_{2} \end{aligned}$ (1.32)

$\begin{aligned} \frac{\vec{\lambda}+\underline{\lambda}}{|\boldsymbol{\Lambda}|} \rightarrow \max \end{aligned}$ (1.33)

Таким образом, ставится задача максимизации расстояния между полупространствами (1.31) и (1.32), содержащими все точки из множеств w₁и w₂ соответственно. Если окажется, что искомый максимум (1.33) отрицательный, то очевидно, что множества w₁и w₂ неразделимы.

Пример нахождения по критерию (1.33) вектора Λ и параллельных гиперплоскостей Н₁ и Н₂, задающих области решений в одной из задач распознавания двух классов электрокардиосигналов (w₁и w₂), приведен на рис. 1.

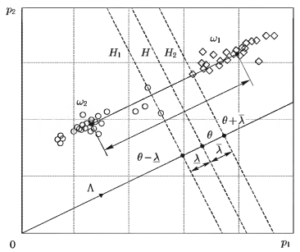
Рис. 1. Результат построения сети для двух сравниваемых цепочек T1 и T2

Здесь два класса сигналов заданы в пространстве спектральных признаков p₁ и p₂. Расстояние между центрами классов обозначено Δ. Результирующее решающее правило (1.30), которое используется в линейном классификаторе, задается гиперплоскостью H.

Если ввести условие нормировки:

$|\Lambda|=\sqrt{\lambda_{1}^{2}+\lambda_{2}^{2}+\ldots+\lambda_{m}^{2}}=1$

задачу (1.31 )-(1.33) можно записать как нахождение

$\max \theta ({\vec{\lambda^{\prime}}+\underline{\lambda'}})$ , (1.34)

при условиях

$\begin{aligned} \boldsymbol{\Lambda}^{\mathrm{'T}} \mathbf{P}_{j} & \geqslant \vec{\lambda}+1, \quad j \in \omega_{1} \end{aligned}$

$\begin{aligned} \mathbf{\Lambda}^{\mathrm{'T}} \mathbf{P}_{j} \leqslant-\underline{\lambda}+\theta, & j \in \omega_{2} \end{aligned}$

где

$\Lambda^{\prime}=\frac{1}{\theta}\Lambda , \quad\vec{\lambda}^{\prime}=\frac{1}{\theta}\vec{\lambda} , \quad\underline{\lambda}^{\prime}=\frac{1}{\theta}\underline{\lambda}$ (1.35)

$\left|\Lambda^{\prime}\right|=\sqrt{\left(\lambda_{1}^{\prime}\right)^{2}+\left(\lambda_{2}^{\prime}\right)^{2}+\ldots+\left(\lambda_{m}^{\prime}\right)^{2}}=\frac{1}{\theta}$ (1.36)

Очевидно, что вместо (1.34) (1.36) можно решать задачу ЛП

$\max ({\vec{\lambda^{\prime}}+\underline{\lambda'}})$ (1.37)

при тех же условиях

$\begin{aligned} \boldsymbol{\Lambda}^{\mathrm{'T}} \mathbf{P}_{j} & \geqslant \vec{\lambda}+1, \quad j \in \omega_{1} \end{aligned}$

$\begin{aligned} \mathbf{\Lambda}^{\mathrm{'T}} \mathbf{P}_{j} \leqslant-\underline{\lambda}+\theta, & j \in \omega_{2} \end{aligned}$

и определить величину θ из (1.36), а искомые коэффициенты — из (1.35). Задачу (1.37) удобно решать, переходя к двойственной задаче линейного программирования². Для этого рассмотрим следующую общую задачу ЛП. записав ее в виде

max(c₁x₁ + c₂x₂ + … + c_nx_n);

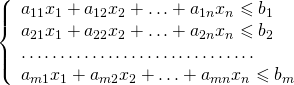$\left\{\begin{array}{l}{a_{11} x_{1}+a_{12} x_{2}+\ldots+a_{1 n} x_{n} \leqslant b_{1}} \\ {a_{21} x_{1}+a_{22} x_{2}+\ldots+a_{2 n} x_{n} \leqslant b_{2}} \\ {\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots} \\ {a_{m 1} x_{1}+a_{m 2} x_{2}+\ldots+a_{m n} x_{n} \leqslant b_{m}}\end{array}\right.$ (1.38)

или в матричной записи:

шах (с, х); Ах ≤ b,

где целевая функция представлена в виде скалярного произведения (с, х) двух векторов х = (x₁, x₂,….,x_n), с = (с₁, с₂…..с_n), а вектор ограничений — в виде матрицы-столбца b = (b₁,b₂…..b_m). Здесь, как и в (1.37), на координаты вектора х не накладывается никаких дополнительных условий.

Двойственной к (1.38) будет задача ЛП от m переменных y₁, y₂, … ,y_m вида

min(b₁y₁ + b₂y₂ + … + b_my_m));

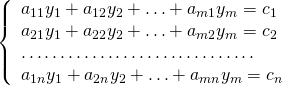$\left\{\begin{array}{l}{a_{11} y_{1}+a_{12} y_{2}+\ldots+a_{m 1}y_{m} = c_{1}} \\ {a_{21} y_{1}+a_{22} y_{2}+\ldots+a_{m 2} y_{m} = c_{2}} \\ {\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots} \\ {a_{1 n} y_{1}+a_{2 n} y_{2}+\ldots+a_{m n} y_{m} = c_{n}}\end{array}\right.$ (1.39)

где $y_{i} \geqslant 0(i=\overline{1, m})$ , или в матричной записи:

min(b, у);

А^Tу = с; у ≥0, где Y = (y₁, y₂, …,y_m).

Как видно в (1.39), переменных столько же, сколько строк в матрице А задачи (1.38). Матрица ограничений в (1.39) транспонированная матрица А. Вектором правой части ограничений в (1.39) служит вектор коэффициентов максимизируемой линейной функции (1.38), при этом знаки неравенств меняются на равенство. Коэффициенты целевой функции в (1.39) задаются вектором правой части ограничений задачи (1.38). При этом символ max меняется на min. На переменные y_i, $i=\overline{1, m}$ накладывается условие неотрицательности.

В соответствии со второй теоремой двойственности оптимальный план X* = (x₁^*,x₂^*, … ,x_n^*) прямой задачи (1.38) однозначно связан с решением двойственной задачи (1.39) у* = (y₁*, y₂*, …,y_m*) ³. Существующую зависимость можно представить следующим образом: если y_i* > 0, то

a_i1x₁* + a_i2x₂* + • • • + a_inx_n* = b_i (1.40)

Это соотношение позволяет получить систему, состоящую из n уравнений, которая используется для нахождения оптимального решения прямой задачи.

Таким образом, если в прямой задаче (1.38) число ограничений m значительно превосходит число переменных n, целесообразно вначале решить двойственную задачу (1.39), а затем перейти к составлению системы уравнений и ее решению относительно неизвестных X* = (x₁^*,x₂^*, … ,x_n^*).

Итак, сформулированную выше задачу отыскания разделяющей гиперплоскости (1.37) можно решить на основе двойственной задачи. Условия ограничения в (1.37) можно привести к виду

-(λ’₁p_1j+λ’₂p_2j + … + λ’_mp_mj) + $\vec{\lambda}^{'}$ ≤ -1, j ∈ w₁ (1.41)

λ’₁p_1j+λ’₂p_2j + … + λ’_mp_mj + $\underline{\lambda}^{'}$ ≤ 1, j ∈ w₂ (1.42)

Здесь неизвестными являются параметры λ’₁,λ’₂,….λ’_m, $\vec{\lambda}^{'}$ , $\underline{\lambda}^{'}$ , оптимальные значения которых входят в уравнения двух параллельных гиперплоскостей. Число ограничений определено количеством объектов, образующих классы w₁и w₂. Оно же задает и число неизвестных x_j, j ∈ w₁, j ∈ w₂ в двойственной задаче.

Следуя правилам построения сопряженных задач (1.38) и (1.39), ее можно представить следующим образом. Найти

$\min ( -\sum_{j \in \omega_{1}} x_{j} + \sum_{j \in \omega_{2}} x_{j})$

при условиях, записанных в виде системы уравнений-ограничений

$\sum_{j \in \omega_{1}}-p_{1 j} x_{j}+\sum_{j \in \omega_{2}}} p_{1 j} x_{j}=0$
$\sum_{j \in \omega_{1}}-p_{2 j} x_{j}+\sum_{j \in \omega_{2}} p_{2 j} x_{j}=0$
$\ldots \ldots \ldots \ldots \ldots \ldots \ldots$
$\sum_{j \in \omega_{1}}-p_{m j} x_{j}+\sum_{j \in \omega_{2}} p_{m j} x_{j}=0$
$\sum_{j \in \omega_{1}} x_{j}=1$
$\sum_{j \in \omega_{2}} x_{j}=1$

где x_j ≥ 0.

В данной задаче имеется лишь m + 2 ограничения, что значительно упрощает ее решение. Обычно число объектов значительно превышает размерность пространства признаков, в котором строится разделяющая гиперплоскость. Если общее число объектов равно я, то число свободных переменных x_j будет равно n – (m + 2). Выразив ?и базисных переменных через выбранные свободные переменные, можно перейти к стандартной форме представления системы уравнений-ограничений. Применение симплекс-метода, основанного на табличном алгоритме замены базисных переменных, позволит найти все множество оптимальных значений (x_j, j ∈ w₁, j ∈ w₂), из которых лишь m + 2 переменных будут иметь ненулевые значения. Если найденный оптимальный план этой задачи представить в виде (x₁^*,x₂^*, … ,x_m+2^* …0,0), то лишь для первых m + 2 переменных будет составлена система уравнений-ограничений прямой задачи следующего вида:

-(λ’₁p_1j+λ’₂p_2j + … + λ’_mp_mj) + $\vec{\lambda}^{'}$ = -1, j ∈ w₁

λ’₁p_1j+λ’₂p_2j + … + λ’_mp_mj + $\underline{\lambda}^{'}$ = 1, j ∈ w₂

Как следует из (1.40). форму равенств приобретают только те неравенства из ограничений (1.41), (1.42), в которых индексы j определяются ненулевыми значениями (x₁^*,x₂^*, … ,x_m+2^*). Решение этой системы уравнений позволяет найти оптимальные значения переменных (λ’₁,λ’₂,….λ’_m, $\vec{\lambda}^{'}$ , $\underline{\lambda}^{'}$ )* и определить вид решающего правила (1.30).

Данный подход показывает возможности применения методов ЛП для построения разделяющих гиперплоскостей в различных задачах медицинской диагностики.

Footnotes

Первозванский А. А. Распознавание абстрактных образов как задача линейного программирования // Изв. Академии наук СССР. Сер. «Техническая кибернетика». 1965. № 4. С. 41-44.
Таха X. А. Введение в исследование операций. 6-е изд. / Пер. с англ. — М.: Вильямс, 2001. — 912 с.
Таха X. А. Введение в исследование операций. 6-е изд. / Пер. с англ. — М.: Вильямс, 2001. — 912 с.