Выравнивание биологических последовательностей (с примерами)

Выравнивание символьных последовательностей

Наиболее важной задачей анализа биологических последовательностей, распознавания биомедицинских сигналов по лингвистическому описанию является их выравнивание. Для двух заданных последовательностей оно означает выполнение ряда преобразований некоторой цепочки символов, обеспечивающее совмещение и сравнение ее с другой цепочкой. При этом длины обеих цепочек становятся равными.

В молекулярной биологии выравнивание используется для анализа межнуклеотидных последовательностей в молекуле РНК, что позволяет решать задачу распознавания стабильной «вторичной» ее структуры. В задачах автоматического анализа биомедицинских сигналов применение структурных методов обработки данных позволяет представить фрагменты сигнала в виде цепочек символов конечного алфавита, а последующее выравнивание становится важным этапом процедуры классификации биосигналов.

Рассмотрим задачу выравнивания двух упорядоченных последовательностей символов Т₁ и Т₂. В начале паре сравниваемых цепочек сопоставим сеть G(Т₁, Т₂), которая строится следующим образом¹. Составим прямоугольную сетку, вертикальные линии которой соответствуют символам цепочки Т₁, а горизонтальные — Т₂. С каждой ячейкой, представляющей собой квадрат с ребром единичной длины, свяжем пару индексов (i, j), где i — порядковый номер символа в Т₁, a j — в цепочке Т₂. Выделим в сети только те ячейки, для которых символы, стоящие на горизонтальной и вертикальной осях, совпадают. В каждой такой ячейке проведем диагональ, связывающую ее левую верхнюю и правую нижнюю вершины. Все вертикальные и диагональные ребра ориентируем стрелкой вниз, а горизонтальные — стрелкой слева направо. Стрелки указывают на все возможные перемещения по узлам сетки.

Множество вершин полученной решетки есть множество вершин графа сети G(Т₁, Т₂), число их равно q = (m + l)(n + 1). где m — число символов в Т₁, n — число символов в Т₂. Множество ориентированных ребер — множество дуг этого графа. Истоком S₀ сети является левая верхняя вершина, а стоком правая нижняя вершина.

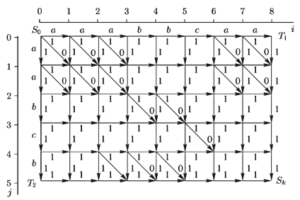
Пусть Т₁ = (a a a b b с a a) и Т₂ = (a а b с b), тогда соответствующая этой паре цепочек сеть G(Т₁, Т₂) примет вид, приведенный на рис. 1. Каждый путь S, ведущий из S₀ в S_k, порождает цепочку элементарных преобразований, переводящих Т₁ в Т₂. При этом движение по левой вертикали ячейки (i, j) означает вставку в соответствующую позицию цепочки Т₁ j-ro символа цепочки Т₂. Движение по верхней горизонтали означает удаление i-го символа в Т₁. Движение по диагонали означает сохранение i-го символа.

Для сети G(Т₁,Т₂) зададим систему весов: каждой вертикальной и горизонтальной дуге определим вес, равный 1, а каждой диагональной дуге — вес, равный 0. Длину пути r(S) будем вычислять как сумму весов дуг, лежащих на этом пути.

Представленная в виде ориентированного графа сеть (рис. 1.30) показывает множество путей Ф(Т₁, Т₂) возможных трансформаций Т₁в Т₂. Длина каждого пути равна числу необходимых при этом элементарных преобразований и, следовательно, значению меры их различия. Наибольший интерес представляют наиболее короткие пути преобразований. Именно они позволяют оценить степень сходства анализируемых цепочек. В качестве меры сходства цепочек Т₁ и Т₂ принимают длину кратчайшего из множества путей Ф(Т₁, Т₂):

$r^{\circ}\left(T_{1}, T_{2}\right)=\min _{\mathbf{S} \in \Phi\left(T_{1}, \mathbf{T}_{2}\right)} r(\mathbf{S})$

Задача нахождения кратчайшего пути может быть решена с использованием метода динамического программирования (ДП).

Прежде чем описать процедуру нахождения наилучшей траектории, дадим формальное определение оптимального выравнивания упорядоченных последовательностей символов. Под выравниванием U = u₁, u₂, … , u_m и V = v₁, v₂, … ,v_m будем понимать последовательность элементарных преобразований, переводящих их в пару цепочек U и V длиной l ≥ max(m, п), в которых нет пустых символов в одинаковых позициях. При этом используются следующие операции редактирования: замена, удаление и вставка символа.

Пусть для любой пары символов α, β определена стоимость δ(α —> β) замены α на β. Замена α —> ε соответствует удалению символа α, а ε —> β — вставке символа β. Стоимостью W(U, V) выравнивания будем называть величину

$W(\tilde{U}, \tilde{V})=\sum_{i=1}^{l} \delta\left(\tilde{u}_{i} \rightarrow \tilde{v}_{i}\right)$ .

Тогда каждая последовательность преобразований получает свою цену. Выравнивание называют оптимальным, если его стоимость минимальна.

Суть рассматриваемой процедуры заключена в вычислении стоимости оптимального выравнивания между всевозможными начальными фрагментами (префиксами) двух сравниваемых слов U и V. При этом задача решается в порядке возрастания длин фрагментов.

Выравнивание префиксов может быть выполнено одним из трех способов:

сопоставлением префиксов длины (i – 1) и (j – 1), а также символов u_i и v_j, что соответствует оставлению символов u_i и v_jв анализируемых последовательностях;
сопоставлением префиксов длины (i – 1) и j, а также символов u_i и ε, что соответствует удалению символа u_i;
сопоставлением префиксов длины i и (j – 1), а также символов ε и v_j, что соответствует вставке символа v_j.

Алгоритм расчета оптимального выравнивания основан на вычислении стоимости редактирования префиксов U и V длины i и j с использованием значений уже известной стоимости, рассчитанной для более коротких префиксов. Обозначим через W_s(i,j), 0 ≤ i ≤ m, 0 ≤ j ≤ n стоимость оптимального выравнивания (u₁, u₂, … , u_i) и (v₁, v₂, … ,v_j). Тогда на каждом шаге продвижения по сети можно использовать следующие рекуррентные соотношения:

W_δ= (0. 0) = 0; (1.43)

W_δ(i + 1, 0) = W_δ(i, 0) + δ(u_i+1 → ε); (1.44)

W_δ(0, j + 1) = W_δ(0, j) + δ(ε → v_{j +1}); (1.45)

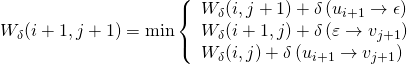$W_{\delta}(i+1, j+1)=\min \left\{\begin{array}{l}{W_{\delta}(i, j+1)+\delta\left(u_{i+1} \rightarrow \epsilon\right)} \\ {W_{\delta}(i+1, j)+\delta\left(\varepsilon \rightarrow v_{j+1}\right)} \\ {W_{\delta}(i, j)+\delta\left(u_{i+1} \rightarrow v_{j+1}\right)}\end{array}\right.$ (1.46)

Здесь W_δ(i, j + 1), W_δ(i + 1, j), W_δ(i, j) стоимости оптимального выравнивания для пар последовательностей меньшей длины. Оно выполнено на предыдущих шагах рассматриваемой процедуры.

В процессе последовательного продвижения по узлам сети в направлении от истока к стоку на каждом шаге производится условная оптимизация управления с использованием стоимости замены δ(u_i+1 → v_{j +1}), вставки δ(ε → v_{j +1}) или удаления δ(u_i+1 → ε) последнего символа анализируемого фрагмента слова U. Как следует из (1.43), стоимость выравнивания пустых слов задается равной нулю. Выражение (1.44) оценивает суммарные затраты при движении по узлам верхней горизонтали сети. Выражение (1.45) связано с оценкой затрат при движении по левой вертикали сети. Соотношение (1.46) используется для условной оптимизации во всех остальных узлах ориентированного графа. При этом для каждого узла сети выбирается то шаговое управление, которое обеспечивает минимум суммарных затрат.

Возвращаясь к задаче выравнивания цепочек Т₁ и Т₂, следует отмстить, что стоимости δ(u_i+1 → v_{j +1}) = 0, δ(u_i+1 → ε) = 1, δ(ε → v_{j +1}) = 1. Используя рекуррентные соотношения (1.43)—(1.46) в процедуре оптимального выравнивания Т₁ и Т₂ в направлении от вершины S₀ в S_k получим ориентированный граф (рис. 1.31). Здесь для каждого узла сетки (i, j), соответствующего промежуточному состоянию S_i,j, стрелками указаны траектории, необходимые для оптимального выравнивания соответствующих последовательностей. Кроме того, в кружках узлов сетки указаны стоимости соответствующих суммарных затрат. Так, для промежуточного узла (i, j) = (4.2) соответствующего выравниванию префиксов Т₁ – {а а а b) и Т₂ – (а а), одна из оптимальных траекторий задается последовательностью вершин графа {S_0,0, S_1,0, S_2,1, S_3,2,S_4,2}. При этом в цепочке {a а а b} вначале удаляется символ а, последующие два символа сохраняются, а последний символ b также подлежит удалению. Напротив, в цепочке {a а} вначале добавляется символ а, последующие два символа сохраняются, а в конце цепочки вставлен символ b. В результате соответствующие префиксы принимают вид $\widetilde{T}_{1}$ = (-, а, а,-) и $\widetilde{T}_{2}$ = (а, а, а, b). Здесь тире обозначают пустые символы, а запятые служат разделителями.

Рис. 1. Результат условной оптимизации выравнивания цепочек Т1 и Т2

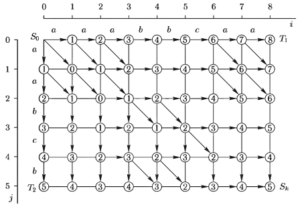
Рис. 2. Результат безусловной оптимизации выравнивания цепочек Т1 и Т2

Рис. 3. Множество оптимальных траекторий перехода из S0 в Sk

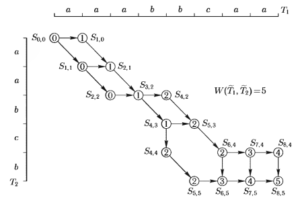
Рис. 4. Первый шаг перехода ТР к блок-схеме алгоритма

Суммарные затраты такого преобразования составляют 2 единицы, что отмечено в кружке конечной для префикса вершины S_4,2. Как следует из рисунка, оптимальная траектория для сравниваемых префиксов оказалась не единственной, но все эквивалентные пути требуют одинаковых затрат.

Затем в соответствии со схемой решения задач ДП строится оптимальная траектория из S₀ в S_k. Она обеспечивает выравнивание полных последовательностей Т₁ и Т₂ с минимальными затратами. Для этого нужно выстроить непрерывную цепочку стрелок перехода из начального состояния в конечное. Результат такой безусловной оптимизации показан на рис. 3.

Как следует из рисунка, возможно целое множество альтернативных траекторий выравнивания слов Т₁ и Т₂ суммарные затраты при этом W( $\widetilde{T}_{1}$ , $\widetilde{T}_{2}$ ) = 5. Эта величина определяет число элементарных преобразований, переводящих цепочку Т₁ в Т₂.

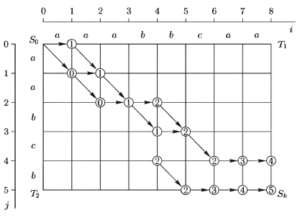
Выделим два способа выравнивания, которые соответствуют верхней и нижней траекториям на сети G(Т₁,Т₂). Результаты такого редактирования приведены в табл. 1.1, а также проиллюстрированы на рис. 4.

Во втором столбце таблицы указана вся последовательность промежуточных шагов, которая приводит к оптимальному выравниванию. Третий столбец содержит упорядоченные последовательности символов, полученные в результате преобразования Т₁ = (a a a b b с а а) и Т₂ = (а а b с b).

Выравнивание цепочки Т₁ по верхней траектории ориентированного графа включает следующую последовательность шагов (рис. 4):

удаление символа а:

$(a \rightarrow \varepsilon) ; S_{0,0} \rightarrow S_{1,0} ; \widetilde{T}_{1}=(-), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=1$

сохранение символа а:

$(a \rightarrow a) ; S_{1,0} \rightarrow S_{2,1} ; \widetilde{T}_{1}=(-, a), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=1$ ;

сохранение символа а:

$(a \rightarrow a) ; S_{2,1} \rightarrow S_{3,2} ; \widetilde{T}_{1}=(-, a, a), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=1$ ;

удаление символа b:

$(b \rightarrow \varepsilon) ; S_{3,2} \rightarrow S_{4,2} ; \widetilde{T}_{1}=(-, a, a,-), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=2$ ;

сохранение символа b:

$(b \rightarrow b) ; S_{4,2} \rightarrow S_{5,3} ; \widetilde{T}_{1}=(-, a, a,-, b), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=2$ ;

сохранение символа с:

$(c \rightarrow c) ; S_{5,3} \rightarrow S_{6,4} ; \widetilde{T}_{1}=(-, a, a,-, b, c), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=2$ ;

удаление символа а:

$(a \rightarrow \varepsilon) ; S_{6,4} \rightarrow S_{7,4} ; \widetilde{T}_{1}=(-, a, a,-, b, c,-), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=3$ ;

удаление символа а:

$(a \rightarrow \varepsilon) ; S_{7,4} \rightarrow S_{8,4} ; \widetilde{T}_{1}=(-, a, a,-, b, c,-,-), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=4$ ;

вставка символа b:

$(\varepsilon \rightarrow b) ; S_{8,4} \rightarrow S_{8,5} ; \widetilde{T}_{1}=(-, a, a,-, b, c,-,-, b), W=\left(\widetilde{T}_{1}, \widetilde{T}_{2}\right)=5$ .

Таблица 1.1

Путь из S₀ в S_k

Траектория

Результат выравнивания Т₁ = (a a a b b с а а) и Т₂ = (а а b с b)

Верхний путь

S_0.0; S_1.0; S_2.1; S_3.2; S_4.2; S_5.3; S_6.4; S_7.4; S_8.4; S_{8. 5}

$\widetilde{T}_{1}$ = (-, a, a,-, b, c,-,-, b)

$\widetilde{T}_{2}$ = (a, a, a, b, b. c, a, a,-)

Нижний путь

S_0.0; S_1.1; S_2.2; S_3.2; S_4.3; S_4.4; S_5.5; S_6.5; S_7.5; S_{8. 5}

$\widetilde{T}_{1}$ = (a, a,-, b, c, b,-,-,-)

$\widetilde{T}_{2}$ = (a, a, a, b,-, b, c, a, a)

Выравнивание Т₂ строится по той же траектории. Отличия заключаются лишь в том, что движение по верхней горизонтали ячейки (i, j) означает вставку символа, стоящего в Т₁ на i-м месте, а движение по левой вертикали — удаление j-ro символа в Т₂.

Как видно из табл. 1.1, длина $\widetilde{T}_{1}$ и $\widetilde{T}_{2}$ в результате трансформации цепочек Т₁ и Т₂ стала одинаковой (l = 9), а пустые символы стоят в них в разных позициях.

Процедура временного выравнивания и оценка W( $\widetilde{T}_{1}$ , $\widetilde{T}_{2}$ ) могут быть использованы в задачах классификации биомедицинских сигналов по их символьному описанию. В том случае, когда цепочка Т₂представляет собой эталонную последовательность символов, которая описывает некоторый класс сигналов, величина W( $\widetilde{T}_{1}$ , $\widetilde{T}_{2}$ ) отождествляется с расстоянием от анализируемой цепочки Т₁ до этого эталона. При наличии нескольких классов сигналов, каждый из которых представлен своим эталоном, по этой величине может быть оценена мера принадлежности данной последовательности каждому из классов.

Footnotes

Браверман Э. Л1., Мучник И. Б. Структурные методы обработки эмпирических данных. — М.: Наука. Гл. ред. физ.-мат. лит., 1983. — 464 с.