Дискретизация и квантование сигналов

Частотный подход к анализу сигналов

Наиболее распространенным подходом к обработке и анализу сигналов является частотный подход, при котором предполагается, что рассматриваемый процесс может быть представлен в виде суммы синусоид с различными частотами. Теоретической базой для частотного подхода является теория преобразований и рядов Фурье¹.

Синусоида полностью определяется формулой x(t) = A sin(2π ft + θ), где А — амплитуда; f — частота; θ — фазовый сдвиг (рис. 1).

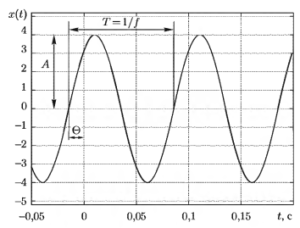
С точки зрения частотного подхода, процедуры цифровой фильтрации решают задачу целенаправленного изменения амплитуды и фазы каждой из частотных составляющих в соответствии с заданной передаточной функцией. В свою очередь, задачей спектрального анализа является количественная оценка параметров синусоид для всего диапазона исследуемых частот.

Дискретное представление непрерывного сигнала и теорема отсчетов

Для обработки и анализа непрерывных сигналов необходимо их преобразование в цифровую форму, которое выполняется при помощи аналого-цифрового преобразователя и может рассматриваться как сочетание двух базовых процедур: дискретизации и квантования.

Дискретизация — взятие измерений (отсчетов) в дискретные моменты времени.

Квантование — присваивание цифровому отсчету значения, соответствующего некоторому фиксированному уровню сигнала.

Компьютерная обработка возможна только для данных, представленных в форме чисел. В случае обработки сигналов это, как правило, последовательность отсчетов, полученная в результате равномерной дискретизации. Равномерная дискретизация обычно выполняется с использованием аналого-цифрового преобразователя (АЦП) и заключается в измерении сигнала через определенный интервал времени.

Пусть x(t) — некоторый непрерывный сигнал. Здесь t — непрерывный аргумент, под которым подразумевается время, хотя в общем случае аргументом может быть и какая-нибудь другая величина. Тогда х(n) = х(nТ) представляет собой результат равномерной дискретизации непрерывного сигнала x(t) . Здесь Т — интервал дискретизации, а n — порядковый номер отсчета.

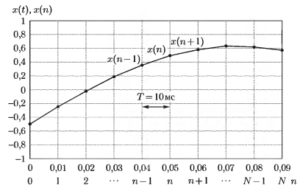
На рис. 2 приведена иллюстрация процесса равномерной дискретизации. В данном случае интервал дискретизации Т = 10 мс = 0,01 с. Величина, обратная интервалу дискретизации (f_n = 1/T), называется частотой дискретизации (в приведенном примере f_n = 1/T = 100 Гц).

Очевидно, что в дискретном сигнале х(n), полученном из непрерывного сигнала x(t), потеряна информация о значениях, лежащих в промежутках между точками взятия отсчетов. В этом случае возникает вопрос: насколько правомерно рассмотрение дискретного сигнала вместо непрерывного? Теоретический ответ на этот вопрос дает теорема отсчетов²³. Эта теорема упоминается в литературе как теорема Котельникова, теорема УКШ (Уиттекера Котельникова Шеннона), теорема Найквиста, что связано с тем, что ее формулировка и доказательство были даны независимо друг от друга несколькими учеными.

Формулировка теоремы отсчетов заключается в следующем: если функция, зависящая от времени, имеет ограниченный частотой F спектр, то она полностью определяется дискретными отсчетами ее значений, следующими с частотой f_n = 2F, и может быть точно реконструирована с помощью выражения

Отметим, что утверждение о возможности полной реконструкции функции является чисто теоретическим, так как основано оно на предположении о бесконечном числе отсчетов дискретного сигнала х(n), что на практике не осуществимо. Тем нс менее, теорема отсчетов является одной из основ всей теории дискретной обработки сигналов.

Нарушение условий теоремы отсчетов проявляется в появлении эффекта наложения частот, который состоит в том, что при выборе недостаточно высокой частоты дискретизации некоторые частотные составляющие становятся неразличимыми.

Классической иллюстрацией эффекта наложения служит восприятие человеком вращения колеса автомобиля, заснятого на кинопленку. При трогании автомобиля с места сначала наблюдается ожидаемое ускорение движения колес. Затем с набором скорости движение колес кажется все медленнее, далее создается впечатление, что колеса остановились совсем и начали вращаться в противоположную сторону. Такая картина объясняется тем, что угловая скорость перемещения регулярных элементов колеса оказывается слишком высокой для того, чтобы при заданной частоте кадров все фазы этого перемещения правильно фиксировались.

Природу возникновения эффекта наложения частот можно продемонстрировать с помощью несложных тригонометрических выкладок⁴.

Пусть заданы три сигнала:

x(t) = cos(2πFt),

x₁(t) = cos[2π(F_д + F)t],

x₂(t) = cos[2π(F_д – F)t],

где F и F_д— некоторые частоты, причем F < ½F_д.

Тогда в результате процедуры равномерной дискретизации с частотой F_д (и периодом Т = 1/F_д) будут соответственно получены следующие три последовательности отсчетов:

x(n) = cos(2πFnT),

x₁(n) = cos[2π(F_д + F)nT],

x₂(n) = cos[2π(F_д – F)nT],

Выполним преобразование:

x₁(n) = cos[2π(F_д + F)nT] = cos[2π( 1/Т + F)nT] = = cos(2πm + 2πFnT) = cos(2πFnT) = x(n).

Аналогично:

x₂(n) = cos[2π(F_д – F)nT] = cos[2π( 1/Т – F)nT] = = cos(2πn – 2πFnT) = cos(2-πFnT)= cos(2πFnT) = x(n).

В приведенных преобразованиях использовались свойства периодичности и четности функции косинус. Оказывается, что x₁(n) = = x₂(n) = x(n). Это означает, что заведомо разные гармонические сигналы x(t), x₁(t) и x₂(t) после их дискретизации с частотой F_д становится невозможно отличить друг от друга.

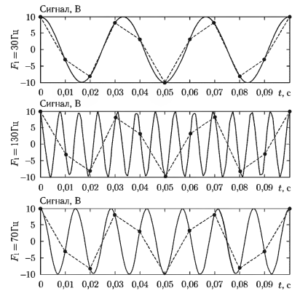
На рис. 3 показан пример, иллюстрирующий приведенные выкладки. На всех трех графиках сплошными линиями показаны сигналы, дискретизованные с частотой F_д1 = 1000 Гц, а пунктирными — с частотой F_д2 = 100 Гц.

На верхнем, среднем и нижнем графиках соответственно показаны синусоиды с частотами: F₁ = 30 Гц, F₂ = F_д2 + F = 130 Гц и F3 = F_д2 – F = 70 Гц.

Из графиков наглядно видно, что нарушение условий теоремы отсчетов приводит к тому, что по отсчетам, взятым с частотой дискретизации F_д2 = 100 Гц, заданные три синусоиды невозможно отличить друг от друга.

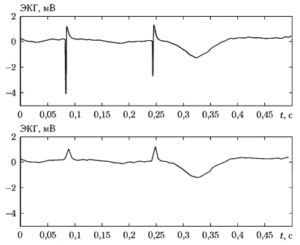
На рис. 4 показан один и тот же фрагмент ЭКГ, содержащий короткие импульсы от элсктрокардиостимулятора, имеющие длительность около 2 мс. На верхнем графике отсчеты взяты с частотой 1000 Гц, а на нижнем — с частотой 125 Гц, которая явно не достаточна для правильного представления данного сигнала. Из графиков видно, что в данном случае налицо потеря важной для медицинской интерпретации сигнала информации, что явилось следствием нарушения условий теоремы отсчетов.

В практических задачах цифровой обработки сигналов использование теоремы отсчетов можно сформулировать в виде следующих основных рекомендаций:

• частота дискретизации должна выбираться так, чтобы она (с запасом нс менее чем в 2 3 раза) превышала верхнюю частоту информативных составляющих сигнала;
• перед аналого-цифровым преобразованием полоса частот исходного аналогового сигнала должна быть ограничена с использованием аналогового фильтра нижних частот с частотой среза намного меньшей, чем половина выбранной частоты дискретизации;
• рассмотрение частотных свойств дискретизованного сигнала оправдано лишь для частот, существенно меньших половины частоты дискретизации.

Квантование сигналов

Как уже отмечалось, квантование — это присваивание отсчету цифрового значения, соответствующего некоторому фиксированному уровню сигнала.

Точность квантования сигнала с использованием аналого-цифрового преобразователя определяется двумя параметрами:

• динамическим диапазоном, задающим пределы измерения входного сигнала;
• разрядностью, определяющей число двоичных разрядов выходного кода АЦП.

Обозначим размах динамического диапазона как А = А_mах – A_min, где А_mах и A_min – наименьшее и наибольшее измеряемые значения непрерывного сигнала на входе АЦП соответственно. Если далее обозначить разрядность АЦП как к, то наибольшее возможное число уровней квантования К = 2^k. а величина а = А/К соответствует дистанции между соседними уровнями квантования и называется шагом квантования.

Шаг квантования определяет точность представления входного аналогового сигнала в виде цифровых отсчетов. Максимальная ошибка квантования зависит от принципа работы АЦП и равняется ±а/2 для АЦП, присваивающего значение ближайшего уровня квантования.

Нетрудно показать⁵, что среднеквадратическая ошибка квантования при этом будет составлять а/√12 « 0,29α.

Для оптимального выбора динамического диапазона АЦП и его разрядности необходима информация о диапазоне возможного изменения сигнала на входе АЦП и о требуемой точности представления цифрового сигнала. Отметим, что повышение точности за счет увеличения разрядности ограничено точностью представления самого аналогового сигнала (например, уровнем собственных шумов усилителя, если на входе АЦП измеряется напряжение или ток).

1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир, 1990. — 584 с.
2. Аифичер Э. С.. Джервис Б. У. Цифровая обработка сигналов: практический подход / Пер. с англ. — М.: ИД «Вильямс», 2004. — 992 с.
3. Хемминг Р. В. Цифровые фильтры. — М.: Сов. радио, 1980. — 224 с.
4. Хемминг Р. В. Цифровые фильтры. — М.: Сов. радио, 1980. — 224 с.
5. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. — М.: Мир, 1978. — 848 с.