Преобразование Фурье, как метод анализа ЭЭГ-сигналов

Преобразования Фурье (англ. fourier transform, fourier transformation) – метод математического преобразования, результатом которого является разложение сигнала на его элементарные составляющие – гармонические колебания разной частоты.¹

Принцип метода

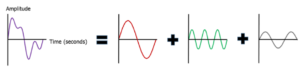
Преобразование Фурье, ЭЭГ, ЭЭГ анализ — Рисунок 1. Комплексный сигнал (фиолетовый, слева) – это сумма отдельных синусоидальных волн (красный, зеленый, серый)

Согласно теории Фурье (см. раздел “математические основы”), любой сигнал можно представить в виде серии синусоидальных волн различной амплитуды и фазы. Например, сигнал на рис.1 в фиолетовом цвете – это просто сумма трех синусоидальных волн.

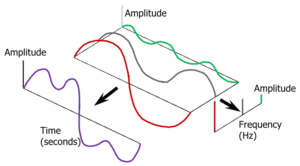
Преобразование Фурье позволяет разложить исходный сигнал на синусоиды. Каждая синусоида имеет соответствующую амплитуду, фазу и частоту (рис. 2).

На рисунке 2 видно, что сложный вид сигнала во временной области может быть представлен всего 3-мя вертикальными линиями в частотной области. Такое упрощенное представление в частотной области помогает идентифицировать ключевые частоты.

Таким образом, преобразование Фурье разбивает сложные временные сигналы на легко понятные частотные составляющие, что позволяет очистить полученный сигнал от шумов и помех, выделить наиболее значимые его компоненты.

Преобразование Фурье делят на несколько видов:²

Непрерывное преобразование Фурье (НПФ) – используется в случае анализа непрерывных сигналов. Данный метод не применим к анализу ЭЭГ, поскольку его реализация возможна только на теоретическом уровне (все сигналы, с которыми ведётся работа на практике являются прерывистыми, т.е. дискретными). Это связано с тем, что реальные процессы ограничены во времени и фиксируются через равные временные промежутки, т.е. дискретны по своей природе. Так, НПФ используют в случае анализа длительно протекающих динамических процессов в научных исследованиях и экспериментах, где частота дискретизации (т.е. минимальная частица измерения) пренебрежимо мала по сравнению с полной длиной графика.
Дискретное преобразование Фурье (ДПФ) – вид преобразования Фурье, при котором работа ведется с дискретными данными. При анализе данных ЭЭГ преобразование Фурье является дискретным, поскольку электромагнитные сигналы записываются в определенный промежуток времени (т.е. не являются непрерывными и прерываются).
- Быстрое преобразование Фурье (БПФ) – вид дискретного преобразования Фурье, представляющий собой набор алгоритмов вычислений, который позволяет уменьшить количество математических действий, относительно классического метода (т.е. простого ДПФ). Результат преобразования остается тем же, однако достигается быстрее по времени.

Математические основы

Математической основой преобразования Фурье является теорема Фурье, утверждающая что любой сигнал X (t) в пределах времени от 0 до Т (где Т — эпоха для анализа Фурье, или эпоха анализа – промежуток времени в ходе которого регистрировался сигнал) может быть разделен на набор простых синусоидальных функций, названных рядом Фурье. При этом, чем больше эпоха, тем больше число гармоник (элементарных составляющих сигнала) и выше частотное разрешение для спектров. Например, для эпохи анализа в 4 секунды частотное разрешение 1/4 = 0,25 Гц. Математически, теорема Фурье выражается следующим образом:

$X(t)=A_{0}+\sum A_{n} \sin \left(2 \pi n f t+\varphi_{n}\right)$ ,

где ∑ — сумма по всем частотам (гармоника); f — собственная частота сигнала f= 1 /Т; φ — фаза; n = 1,2,3; A_n— амплитуда; φ_n— фаза синусоидальной компоненты (n — порядок гармоники).

Реализация метода

На сегодняшний день преобразование Фурье применяется преимущественно в целях научного исследования и не распространено в практической медицине. Причиной этого является сложность реализации метода в условиях отсутствия оптимизированного программного обеспечения, интегрированного в систему аппаратного комплекса ЭЭГ.

При необходимости провести преобразование электромагнитного сигнала Фурье наиболее часто используют среду программирования MATLAB³⁴⁵ (рисунок 3).

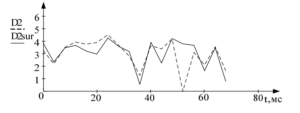
Помимо среды программирования MATLAB применение находит программный комплекс для анализа временных рядов TISEAN (сокр. От Time Series Analysis).⁶⁷ Графики, построенные на основе обработки ЭЭГ пакетом TISEAN, представлены на рисунках 4 и 5.

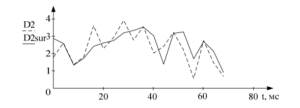
Иллюстрации взяты из работы, в которой проводился автокорреляционный анализ ЭЭГ-сигналов с целью установления их хаотической природы. Для снижения погрешности, вызванной зашумлением, проводилась предварительная “очистка” сигнала с помощью преобразования Фурье. График автокорреляции изначального сигнала представлены на рисунке штриховой линией, очищенного – сплошной. На основании полученных результатов, авторы работы делают вывод о том, что в дальнейшем анализе разумнее использовать те фрагменты ЭЭГ, графики которых совпадают с графиками очищенных сигналов.

Недостатки метода

Возникновение спектральной утечки – явления, сущность которого состоит в распределении мощности спектральных составляющих по диапазону частот. Это приводит к появлению новых частот, которых нет в изначальном сигнале, т.е. мощности реальных частот “просачиваются” в другие диапазоны.
Несомненно, недостатком метода является его недостаточная изученность, ограничивающая его информативность.

Практическое применение

В результате Фурье-преобразования получают спектральный состав суммарной ЭЭГ. Спектральный состав — доля (в %) каждого частотного диапазона в общей мощности ЭЭГ сигнала. Спектральный состав позволяет количественно оценить соотношение активности (ритмов) различных диапазонов частот. После спектральной оценки ЭЭГ сигнала можно определить вклад каждого частотного компонента в основной ритм.

➥ Читайте подробнее: Спектральнй анализ ЭЭГ

С помощью преобразования Фурье осуществляют фильтрацию ЭЭГ-сигнала, в результате чего обнаруженные в сигнале посторонние шумы, артефакты вырезаются, и перед специалистом предстает новый очищенный ЭЭГ-сигнал, где наиболее наглядно отражены его основные компоненты.

Применяется преобразования Фурье на сегодняшний день для :

Изучения и оценки глубины анестезии;⁸
Изучения, обнаружения, прогнозирования и классификации эпилептических припадков;⁹¹⁰
Изучения сонных веретен и спайко-волновых разрядов на ЭЭГ;¹¹
Обучения и составления нейронных сетей.¹²

Значимость анализа ЭЭГ методом преобразования Фурье остается не ясной. По данным некоторых исследований, изучение метода преобразования Фурье в ЭЭГ имеет достаточно спорные и неоднозначные результаты, не дающие полного ответа на вопрос о практической значимости метода. Ряд ученых придерживается позиции, что метод преобразования Фурье вовсе не является информативным, поскольку изначально электромагнитные сигналы головного мозга не имеют синусоидальную природу¹³. Некоторые, наоборот, опровергают эту точку зрения, полагая, что преобразование патологических паттернов методом преобразования Фурье помогает проще визуализировать их, и, соответственно, найти нарушения в работе головного мозга раньше, чем появятся клинические признаки.¹⁴

В заключение можно сказать, что анализ ЭЭГ методом преобразования Фурье требует дополнительного детального исследования, с последующим выявлением закономерности между новыми и уже полученными результатами.

Footnotes

Сахаров В.Л. «Методы и средства анализа медико-биологической информации: Учебно-методическое пособие» Таганрог: Изд-во ТРТУ, 2001. 70 с.
[Электронный ресурс]
Калиниченко А.Н., Манило Л.А., Немирко А.П., Волкова С.С. (2010). Оценка глубины анестезии по ЭЭГ на основе спектральной энтропии. Биотехносфера, (3), 27-34.
Кучерик А.О, Кутровская С.В., Бухаров Д.Н. Методические указания для выполнения лабораторных работ по дисциплине «Обработка и анализ сигналов и сцен», Владимир, 2016. – с.21-26.
Samiee K, Kovács P, Gabbouj M. Epileptic seizure classification of EEG time-series using rational discrete short-time fourier transform. IEEE Trans Biomed Eng. 2015;62(2):541-552. doi:10.1109/TBME.2014.2360101
Душенин, Д. Ю. (2010). Анализ применимости методов нелинейной динамики к ЭЭГ-мониторингу. Известия Южного федерального университета. Технические науки, 109 (8), 55-60.
Hegger R., Kantz H., Schreiber T. Practical implementation of nonlinear time series methods: The TISEAN package, CHAOS 9, 413 (1999).
Калиниченко А.Н., Манило Л.А., Немирко А.П., Волкова С.С. (2010). Оценка глубины анестезии по ЭЭГ на основе спектральной энтропии. Биотехносфера, (3), 27-34.
Vidyaratne LS, Iftekharuddin KM. Real-Time Epileptic Seizure Detection Using EEG. IEEE Trans Neural Syst Rehabil Eng. 2017;25(11):2146-2156. doi:10.1109/TNSRE.2017.2697920
Truong ND, Nguyen AD, Kuhlmann L, et al. Convolutional neural networks for seizure prediction using intracranial and scalp electroencephalogram. Neural Netw. 2018;105:104-111. doi:10.1016/j.neunet.2018.04.018
Sitnikova E, Hramov AE, Koronovsky AA, van Luijtelaar G. Sleep spindles and spike-wave discharges in EEG: Their generic features, similarities and distinctions disclosed with Fourier transform and continuous wavelet analysis. J Neurosci Methods. 2009;180(2):304-316. doi:10.1016/j.jneumeth.2009.04.006
Ha KW, Jeong JW. Motor Imagery EEG Classification Using Capsule Networks. Sensors (Basel). 2019;19(13):2854. Published 2019 Jun 27. doi:10.3390/s19132854
Diagnostic and therapeutic technology assessment. Quantitative EEG (Fast Fourier Transform Analysis) monitoring. JAMA. 1983;250(3):420
Rampil IJ. Fast Fourier transformation of EEG data. JAMA. 1984;251(5):601.