Оценка параметров дыхания при искусственной вентиляции легких
Аппараты искусственной вентиляции легких (ИВЛ) являются основными жизнеобеспечивающими приборами, которыми оснащены все отделения реанимации и интенсивной терапии. Основное назначение аппаратов ИВЛ — снабжение легких пациента необходимой для дыхания газовой смесью и вывод из них углекислого газа и других компонентов воздушной смеси. Данная функция аппаратов ИВЛ носит название «протезирование дыхания» и является абсолютно необходимой для сохранения жизни пациентам в раннем послеоперационном периоде, в коматозном состоянии и других клинических ситуациях, когда они не способны дышать самостоятельно1.
Искусственная вентиляция легких является сложной проблемой как с технической точки зрения, так и с позиций физиологии. Кроме того, задачи, решаемые аппаратами ИВЛ, и условия их применения весьма разнообразны. Подробно эти вопросы описываются в специальной литературе23. Здесь мы рассмотрим только наиболее общие вопросы, связанные с применением методов цифровой обработки сигналов в аппаратуре для ИВЛ.
Важнейшими параметрами, характеризующими процесс искусственной вентиляции легких, являются поток, объем и давление газа4. Наиболее часто поток (F) принято выражать в литрах в минуту, объем (V’) — в миллилитрах, а давление (Р) — в сантиметрах водного столба (см вод. ст.), хотя находят применение и альтернативные единицы измерения5. Характер изменения указанных трех параметров в течение дыхательного цикла зависит от установленного режима ИВЛ, состояния органов дыхания пациента, наличия у пациента спонтанной (собственной) дыхательной активности и ряда других факторов. Рассмотрим два наиболее часто применяемых режима ИВЛ: режим с заданным давлением и режим достижения заданного объема. Для упрощения будем считать, что спонтанная дыхательная активность пациента отсутствует, то есть дыхание происходит только под управлением аппарата ИВЛ.
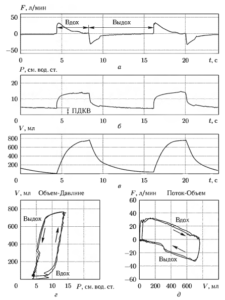
В режиме с контролируемым давлением основным управляемым параметром является давление. В начальный момент цикла дыхания открывается впускной клапан, через который газ подастся в легкие, и начинается наполнение легких газом (фаза вдоха). При этом аппарат контролирует величину давления и не позволяет ей превысить установленное значение. Фаза вдоха завершается по истечении заданного промежутка времени, после чего впускной клапан закрывается и одновременно открывается выпускной клапан, благодаря чему газ начинает выходить из легких за счет упругости грудной клетки (фаза выдоха). Время, отведенное на фазу выдоха, также является устанавливаемым параметром. На рис. 1 (а, б, в) показаны кривые изменения потока, давления и объема при данном режиме ИВЛ.
В данном примере были установлены следующие основные параметры режима ИВЛ:
- частота дыхания — 5 циклов в минуту (продолжительность цикла — 12 с);
- отношение: время вдоха/время выдоха — 1:2;
- максимальное давление 10 см вод. ст.;
- положительное давление конца выдоха (ПДКВ) 4 см вод. ст.
Помимо кривых, показывающих изменение потока, давления и объема. широкое применение находят двумерные графики, попарно связывающие мгновенные значения объема и давления (рис. 1, г) и потока и объема (рис. 1. д), называемые петлями «Объем-Давление» и «Поток Объем» соответственно. Специалисты могут по характеру этих изображений получить важную и достаточно полную информацию как о ходе ИВЛ, так и о состоянии органов дыхания пациента. В связи с этим, во всех промышленно выпускаемых аппаратах ИВЛ предусматривается визуальное отображение данных петель наряду с одномерными (скалярными) графиками каждого из трех параметров в отдельности. Следует отметить, что при построении петель информация о ходе процесса ИВЛ во времени теряется.
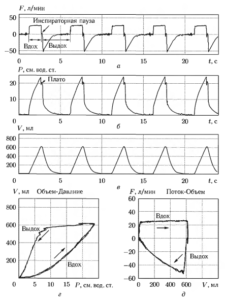
В режиме достижения заданного объема управляемыми параметрами являются поток и объем. В начальный момент цикла дыхания открывается впускной клапан и начинается наполнение легких газом (фаза вдоха). При этом аппарат контролирует величину потока и не позволяет ей превысить установленное значение. Фаза вдоха завершается по достижении установленного объема газа, который рассчитывается в текущем режиме путем интегрирования значений потока, после чего впускной клапан закрывается и фаза вдоха завершается. Далее может следовать короткий промежуток времени, в течение которого закрыты оба клапана (так называемая «инспираторная пауза»). После этого открывается выпускной клапан, и начинается фаза выдоха, которая завершается по прошествии определенного промежутка времени.
На рис. 2 (а, б, в) показаны кривые изменения потока, давления и объема при данном режиме ИВЛ, а также петли «Объем-Давление» (г) и «Поток Объем» (д). В данном примере были установлены следующие основные параметры режимы ИВЛ:
- частота дыхания 12 циклов в минуту (продолжительность цикла — 5 с);
- отношение: время вдоха/время выдоха — 1:2;
- максимальный объем — 600 мл;
- положительное давление конца выдоха (ПДКВ) — 0 см вод. ст.
Отметим характерный вид кривой давления в фазе выдоха: в промежутке времени между закрытием впускного клапана и открытием выпускного (т. е. во время инспираторной паузы) происходит процесс выравнивания давления в системе аппарат-легкие, сопровождающийся экспоненциальным самопроизвольным снижением давления до некоторого значения, которому соответствует небольшой уступ на кривой давления, называемый «плато» (см. 2, б).
Основными спирометрическими показателями, отражающими состояние дыхательной системы при ИВЛ, являются: растяжимость или комплайенс С, а также сопротивление дыхательных путей или резистанс R. Растяжимость определяется как способность к изменению объема на единицу изменения давления:
![]()
где ΔV и ΔР — соответственно приращения объема газа и давления за некоторый промежуток времени. Комплайенс выражается в миллилитрах, деленных на сантиметр водного столба. Резистанс определяется величиной давления, которое необходимо приложить для проведения по дыхательным путям единицы газового объема в единицу времени:
![]()
где F — величина потока газа. Резистанс выражается в сантиметрах водного столба, умноженных на секунду.
В случае использования режима искусственной вентиляции в режиме достижения заданного объема, расчет резистанса и комплайенса может базироваться на оценке изменения давления в промежутке времени между закрытием клапана вдоха и открытием клапана выдоха. Если обозначить уровень давления, на котором завершился предшествующий выдох РEEхр, пиковое давление, достигаемое к концу вдоха —РPeak а давление в конечной точке плато (инспираторной паузы) — PPtato то указанные два показателя могут быть рассчитаны следующим образом6:
С = Vt /(PPtato– РEEхр),
R = (РPeak – PPtato)/F
Здесь VT — это максимальный объем в момент завершения выдоха, a F — установленная для данного режима величина потока.
При известных значениях аэродинамического сопротивления дыхательных путей R и растяжимости легких С может быть рассчитана постоянная времени, также являющаяся одним из важнейших показателей, характеризующих процесс ИВЛ:
τ = CR.
Исходными данными для алгоритма вычисления параметров (таких, как комплайенс, резистанс и постоянная времени) служат синхронно зарегистрированные сигналы, а также отметки времени, соответствующие моментам начала вдоха, окончания вдоха и начала выдоха7. На первом этапе обработки сигналы потока, давления и объема подвергаются предварительной фильтрации с использованием цифрового фильтра нижних частот. С целью обеспечения устойчивости вычисления параметров вентиляции, методом синхронного накопления выполняется формирование текущей усредненной модели каждого из трех сигналов. Усреднение выполняется по нескольким последним дыхательным циклам. При этом каждый раз оценивается срсднеквадратическое отклонение очередного цикла от текущей усредненной модели. В случае, если это отклонение превышает заданный порог, соответствующий цикл не используется для усреднения. Это позволяет обеспечить устойчивость процедуры усреднения сигналов к возможным случайным отклонениям и помехам. По полученной усредненной кривой, используя отметки времени, соответствующие моментам переключения клапанов аппарата, определяют необходимые для расчета величины РEEхр, РPeak и PPtato по которым рассчитываются искомые параметры С, R, и τ.
В тех режимах вентиляции, когда в сигнале давления отсутствует плато (т. е. длительность инспираторной паузы равняется нулю), описанный выше способ расчета использовать нс удается. Кроме того, данный способ позволяет получить только одно значение каждого из этих параметров, соответствующее инспираторной паузе. В то же время известно, что на протяжении всего цикла дыхания эти параметры не остаются постоянными, и информация об их динамике представляет большую диагностическую ценность89.
Более универсальным является подход, основанный на предположении, что общее давление представляет собой сумму давления в дыхательных путях и давления в легких:
P(t) = P1(t) + P2(t) = F(t)R+V(t)/C.
Тогда для двух моментов времени /| и имеем систему из двух уравнений:

Измерив поток, давление и объем в моменты времени t1 и t2 и решив данную систему уравнений, можно вычислить комплайенс С и резистанс R.
Оценка значений комплайенса и резистанса осложняется неустойчивостью сигнала, помехами и наличием спонтанного дыхания. При этом само значение комплайенса меняется на протяжении фазы вдоха. Поэтому его необходимо оценивать по близко расположенным точкам. Для удаления помех из сигнала можно воспользоваться усреднением, фильтрацией или аппроксимацией полиномом. Однако использование фильтра нижних частот для устранения помех приводит к сглаживанию участков начала и окончания вдоха, то есть к искажению сигнала, которое может вызвать появление ошибок расчета параметров дыхания. При синхронном усреднении в сигнале остаются тс помехи, которые связаны с особенностями аппаратуры и одинаковы для всех циклов вдоха. Оба этих недостатка могут быть устранены при использовании полиномиальной аппроксимации. Однако при этом встает вопрос о выборе наиболее оптимального набора конкретных параметров данной процедуры: степени полинома, длительности аппроксимируемого фрагмента, шага перемещения фрагмента. В работе10 показано, что наилучшие результаты удастся получить при следующем наборе параметров алгоритма:
- число усредняемых циклов дыхания — 5-10;
- длительность аппроксимируемого фрагмента 0,4 – 0,6 с;
- шаг перемещения фрагмента 0,05 – 0,1 с;
- дистанция между парой точек для решения системы уравнений — 0,06 – 0,08 с;
- порядок аппроксимирующего полинома — 2.
На рис. 3 показан пример использования аппроксимации полиномом в сравнении с методами, основанными на фильтрации и усреднении. Как видно из данного рисунка, в случае применения полиномиальной аппроксимации обеспечивается наилучшая стабильность вычисления комплайенса и резистанса.
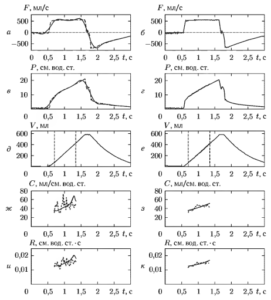
а), в), д) сигналы потока, давления и объема, пунктир — исходные сигналы, сплошная линия — сигналы после ФНЧ; б), г), е) сигналы потока, давления и объема, пунктир — исходные сигналы, сплошная линия — сигналы после процедуры синхронного усреднения; жирной линией показан фрагмент аппроксимации полиномом степени 2; ж), и) рассчитанные значения комплайенса С и резистанса R, пунктир — по исходным сигналам, сплошная линия — с использованием ФНЧ; з), к) рассчитанные по усредненному сигналу значения комплайенса и резистанс, пунктир — по усредненным сигналам, сплошная линия — с использованием полиномиальной аппроксимации
Автоматический анализ формы спирографических петель по их сигнатурам
Контроль состояния пациента в режиме искусственной вентиляции легких (ИВЛ) основан на динамической оценке ряда спнрографических показателей, которые характеризуют эффективность газообмена. К ним в первую очередь относят такие параметры вентиляции, как жизненная емкость легких, сопротивление дыхательных путей, растяжимость легких. В современных аппаратах ИВЛ, обеспечивающих функцию «протезирования дыхания», требуется также реализация диагностических функций, позволяющих на ранних стадиях обнаруживать развитие состояний, угрожающих жизни пациента. К ним можно отнести, например, отек легких, обструктивные нарушения в бронхолегочной системе пациента1112.
Ранняя диагностика патологий органов дыхания возможна лишь в ходе непрерывного контроля за состоянием пациента. Она основана на автоматическом анализе основных параметров внешнего дыхания, а также обнаружении существенных отклонений в заданных режимах ИВЛ. Такой анализ осуществляется по спирографическим кривым, включающим как скалярные функции (давление, поток и объем), так и двумерные функции, представленные в виде петель «объем-давление» (ОД) и «поток-объем» (ПО). В исследованиях, посвященных автоматическому анализу спирограмм при ИВЛ, рассматриваются процедуры измерения параметров вентиляции легких по скалярным кривым, а петли привлекаются только для визуального пояснения наблюдаемых изменений131415. В то же время установлено, что этот вид спирограмм представляет наибольший практический интерес для задач мониторинга в процессе проведения респираторной поддержки.
В работах16 17 предложены методы и алгоритмы непрерывного контроля функций внешнего дыхания по спи рографи четким петлям, в частности, по петлям ОД. Они основаны на динамическом анализе ряда числовых характеристик, которые связаны с основными спирометрическими параметрами (Compliance и Resistance). Применение их в аппаратах ИВЛ позволит более точно регулировать параметры вентиляции и своевременно диагностировать развитие патологий.
Петли «объем—дыхание»
Петля ОД является графической формой описания функциональной зависимости дыхательного объема V от давления р в контуре системы дыхания. В ходе регистрации кривых петля образуется на протяжении каждого дыхательного цикла. Она одновременно отражает влияние двух физиологических параметров: растяжимости легких С (Compliance) и сопротивления дыхательных путей R (Resistance). Типичная кривая ОД при ИВЛ с управляемым объемом для одного дыхательного цикла изображена на рис. 4.
Точка А соответствует началу вдоха (концу выдоха), точка В концу вдоха (началу выдоха), а величина VT показывает дыхательный объем легких. Ввиду того, что существует запаздывание изменения объема V относительно давления р, график имеет вид петли гистерезиса. Нижняя ветвь петли связана с работой дыхания по растяжению

Поскольку давление в конце выдоха должно поддерживаться на заданном уровне, кривая дыхания смещена вдоль оси давления р на положительную величину PEEP(Positive End-Expiratory Pressure).
Линия, соединяющая две характерные точки кривой (A, В), задает направление основной оси петли. Наклон оси, равный углу α, характеризует динамическую растяжимость дыхательной системы С = tg α, а ширина петли r — сопротивление дыхательных путей R. При этом расстояния от оси петли до ее восходящей и нисходящей ветвей (на рис. 4 указано стрелками) отражают инспираторное Rи и экспираторное Rэ, сопротивления соответственно. Кроме горизонтальной протяженности петли к с изменением величины сопротивления дыхательных путей связан другой интегральный параметр — площадь петли S, в фазе выдоха (на рис. 4 отмечено штриховкой).
Наблюдение за динамикой формы петли, положением кривой на плоскости, углом наклона а и шириной петли к позволяет косвенно судить об изменениях основных спирометрических показателей С и R, описывающих работу дыхания пациента1819.
На рис. 5 в качестве примера изображены две спирограммы пациентов, зарегистрированные в условиях клиники, для случаев нормы (рис. 5, а) и наличия острого респираторного дистресс-синдрома — ОРДС (рис. 5, б).
Можно заметить, что при патологии изменяются форма, размеры петли, расположение ее на плоскости. На кривой ОД наблюдается отклонение петли к горизонтальной оси (снижается растяжимость легких С) и расширение ее вдоль оси давления (повышается сопротивление дыхательных путей R).
Анализ формы петель по их сигнатурам
Существуют различные способы описания формы петель. Они основаны на использовании цепных кодов, аппроксимации фигур полиномами разных степеней, описании границ набором числовых признаков (площадь, длина, направление главных осей замкнутой фигуры и т.д.), представлении двумерных кривых в виде сигнатур20. Преимуществом сигнатур является то, что описание двумерных петель сводится к более простым одномерным функциям.
Наиболее простой способ получения сигнатуры петли состоит в построении зависимости расстояния от центроида петли до границ кривой в виде функции угла θ с применением равномерной дискретизации по углу (во всех экспериментах Δθ = 1°). Анализ изменений формы петель по сигнатуре предполагает независимость ее от поворота и размера петель. Первое условие достигается выбором фиксированной начальной точки отсчета сигнатуры, например точки начала дыхательного цикла (точка А рис. 4). Тогда можно сравнивать формы петель по скалярным кривым, поскольку они будут синхронизированы с фазами дыхательного цикла. Инвариантность функции к размеру петли обеспечивается нормировкой сигнатуры по максимальному значению или диапазону изменения ее ординат.
Используя цифровое изображение петли, а также функцию сигнатуры, можно вычислить ряд параметров, характеризующих форму и расположение петли на плоскости, провести сравнительный анализ регистрируемой и опорной петли. В качестве опорных петель необходимо выбрать те, которые отражают установленный врачом режим вентиляции легких. В процессе непрерывного контроля опорные кривые могут периодически обновляться, что связано с необходимостью корректировки параметров вентиляции.
Алгоритм динамического анализа петель «объем—давление» по их сигнатурам
Алгоритм динамического анализа петель ОД и распознавания отклонений в режиме ИВЛ можно представить следующим образом.
Вначале проводится нормировка каждой из координатных осей (V и р) с тем, чтобы, во-первых, перейти к безразмерным величинам и, во-вторых, получить расположение петель на плоскости в соответствии с графическим отображением линии нормальной динамической растяжимости легких. Как известно, эта линия должна располагаться так, чтобы значению растяжимости 65 мл/см вод. ст. соответствовал угол наклона α оси петли 45°21. Поэтому при построении сигнатуры нами использована нормировка в виде VК = V/V* и pK= р/р*, где нормирующие величины V* = 1300 мл, р* = 20 см вод. ст.
Далее выполняется обработка нормированных петель (построение сигнатуры, ее нормировка и смещение по оси θ), вычисление и сравнительный анализ параметров, характеризующих особенности формы спирографических кривых. В качестве этих параметров выбраны:
- направление основной оси анализируемой петли ОД (tgα) и угловое отклонение от оси опорного дыхательного цикла (Δα);
- среднеквадратическое отклонение σk сигнатуры;
- ширина петли r и оценка площади петли ОД в фазе выдоха 5Э;
- выраженность артефактов La.
Режим слежения позволяет фиксировать отклонения этих признаков на значение, превышающее некоторый заданный в процентном отношении порог. Как показали эксперименты, сравнение петель целесообразно проводить по усредненным кривым, полученным путем их синхронного накопления. В этом случае значительно снижается влияние помех на качество анализа.
Наклон оси петли tg α является оценкой динамической растяжимости легких С = tg α. Если измерять угловое отклонение Δα, то можно оценивать степень изменения динамического Compliance. Введение порога для Да позволяет обнаруживать патологические изменения, связанные с резким увеличением или уменьшением растяжимости легких.
Среднеквадратическое отклонение сигнатуры используется в качестве оценки изменения формы петли относительно опорной кривой. Оно вычисляется в виде
![]()
где rθ*— отсчеты сигнатуры опорной петли; rkθ — отсчеты сигнатуры для fc-ro порядкового дыхательного цикла; θ = 1 …360; n — размер выборки (п = 360).
Фактически данный параметр оценивает ошибку, связанную с отклонением в форме петель. Введение порога для величины σk позволяет выявить существенные отклонения в заданных режимах ИВЛ.
Сопротивление дыхательных путей можно оценивать одним из двух способов. Первый основан на измерении ширины петли r на уровне середины осевой линии. Второй способ предполагает вычисление площади фигуры Sэ. Учитывая трудности интерпретации измеренных отклонений в случае изменения размеров петли (что связано, например, с необходимостью увеличения VT при ИВЛ), необходимо использовать дополнительную нормировку петель, например по максимальным значениям объема VT и давления рmах опорной петли. В этом случае опорная петля, условно считающаяся «нормой», располагается по линии нормальной динамической растяжимости, а изменения параметров r и Sэ, подлежат сравнению даже при изменении параметров управления вентиляцией легких.
Показатель выраженности артефактов рассчитывался в виде La = L2/S, где L — длина контура петли, S — площадь. Динамическая оценка его важна для выявления значительных колебаний контура петли, что связано с влиянием различных факторов (изменение тонуса мышц пациента, наличие препятствий в дыхательном контуре).
Экспериментальные исследования
Проведено моделирование алгоритма автоматического анализа петель ОД с применением специально разработанной программы, в основе которой лежит функция signature22. В качестве входных сигналов использовались:
- модельные кривые, полученные путем перевода спирографических изображений в цифровую форму (12 записей)23;
- сигналы, полученные на аппарате ИВЛ механическим моделированием изменений растяжимости С и сопротивления R (23 записи);
- реальные записи спирограмм, зарегистрированные в клинике в условиях ИВЛ (слирограммы 15 пациентов).
Реальные данные включали как выборку записей без патологий (5 записей), так и сигналы с тяжелыми нарушениями органов дыхания: ОРДС (К) записей) и обструкция дыхательных путей (5 записей). Эти нарушения были рассмотрены в качестве основных при разработке алгоритма распознавания патологий.
Процесс обработки изображений, исходно представленных в виде битовых матриц, включал в себя следующие этапы: получение описания изображения в виде траектории единичной толщины; приведение описания изображений к фактическому масштабу, указанному для исходных графиков; нахождение узловых точек кривых; интерполяция петель кубическими сплайнами и получение сигналов в виде последовательностей равномерно дискретизованных отсчетов. По двумерным нормализованным кривым определялись две опорные точки (начало и конец вдоха), по которым оценивался угол наклона петли а. Далее вычислялась функция сигнатуры и по ней путем сравнения одномерных описаний двух петель (анализируемой и опорной) определялись величины σk и r.
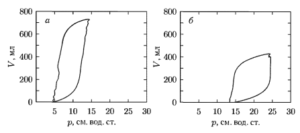
В качестве примера на рис. 6 и 7 представлены реальные петли ОД. На рис. 6, а, в, рис. 7, а, в приведены спирографические кривые; на рис. 6, б, г, рис. 7, б, г — сигнатуры петель. На каждом рисунке нижние кривые соответствуют нормальной форме спирограмм и являются опорными. Верхние петли, имеющие патологические отклонения, сравниваются с ними.
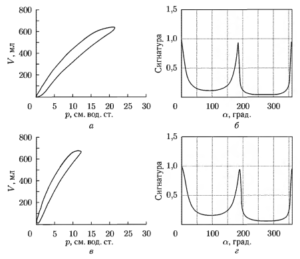
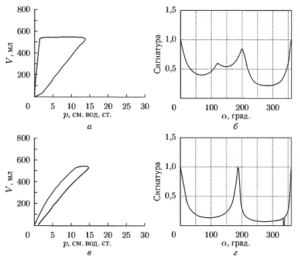
На рис. 6 приведены петли ОД для случая снижения величины Compliance, что вызывает поворот верхней петли вправо. Это изменение обусловлено тем, что для достижения данного уровня объема дыхания (650 мл) требуется большее давление. Подобный вид петель можно наблюдать на поздних стадиях ОРДС. Наблюдаемое снижение величины Compliance может происходить как постепенно, при развитии легочных заболеваний, так и внезапно — при острых нарушениях. На рис. 7 показан случай расширения петли ОД, что вызвано повышением сопротивления дыхательных путей на выдохе, причем инспираторные участки двух кривых аналогичны. Возможными причинами таких отклонений может быть появление нарушений проходимости (обструкция дыхательных путей).
Из сравнения числовых характеристик петель следует, что в первом случае (рис. 6) наблюдается снижение растяжимости легких (Δα = -15°), а во втором (рис. 7) наклон петли сохраняется (Δα = 2°), но изменяется форма петли. Чем больше отличия в форме петель, тем большие значения получает критерий среднеквадратического отклонения. В нашем случае величина σ=0,31 превышает пороговое значение, равное 0,2. Это связано с резким расширением петли (Δr = 0,96) и увеличением ее площади (ΔSэ= 0,08).
Распознать эти опасные нарушения на ранних стадиях можно, используя полученные характеристики. Резкое уменьшение угла наклона а осевой линии петли ОД свидетельствует об увеличении жесткости легких и указывает на развитие ОРДС. Резкое увеличение σ, а также значений параметров r и Sэ свидетельствует о развитии обструкции дыхательных путей.
Проведены эксперименты по оценке эффективности распознавания различных форм петель (реальные записи спирограмм) и обнаружению значимых изменений динамической растяжимости С и сопротивления R дыхательных путей (модельные сигналы). При моделировании спирограмм задавались разные значения Compliance и Resistance, что обеспечило возможность контроля изменений этих параметров. Результаты экспериментов на реальных записях показали, что во всех 15 случаях были безошибочно распознаны нарушения: ОРДС и обструкция дыхательных путей. В ходе экспериментов на модельных сигналах (30 испытаний) удалось безошибочно распознать кривые с измененной формой петли ОД, а также с отклонениями в динамической растяжимости легких. И только в 2 случаях из 30 (6,7 %) не удалось зафиксировать отклонения величины сопротивления дыхательных путей. Анализ записей показал, что эти ошибки связаны с заданием слишком малых величин управляемого потока.
Кроме того, проведен анализ статистической зависимости между заданными величинами R и вычисленными оценками Resistance: r, rэ, Sэ . Значения попарных коэффициентов корреляции к оказались достаточно высокими для всех трех параметров (k > 0,85), однако наибольшее значение k = 0,91 получено для параметра г. Следовательно, именно данный параметр наиболее важен для контроля значимых изменений Resistance по петлям ОД.
В результате проведенных исследований разработан комплекс программ автоматического анализа спирограмм, который предназначен для использования в аппаратах ИВЛ для расширения их диагностических возможностей.
Footnotes
- Mehta S.. Hill N. S. Noninvasive ventilation // Am J Respir Crit Care Med. 2001. Feb. 163(2). P. 540 577.
- Лебединский К. М., Мазурок В. Л., Нефедов Л. В. Основы респираторной поддержки. — СПб.: Изд-во МАЛО, 2006. — 213 с.
- Царенко С. В. Практический курс ИВЛ. — М.: Мединина, 2007. — 160 с.
- Дуда 3., Харт П. Распознавание образов и анализ сцен / Пер. с англ. — М.: Мир, 1976. – 511 с.
- Rapid Interpretation of Ventilator Waveforms / J. B. Waugh, V. M. Deshpande, M. K. Brown, R. J. Harwood. — N. J.: Upper Saddle River, 2007. — 151 p.
- Лебединский К. М., Мазурок В. Л., Нефедов Л. В. Основы респираторной поддержки. — СПб.: Изд-во МАЛО, 2006. — 213 с.
- Калиниченко Л. Н„ Немирно Л. П., Соломонова И. С. Использование полиномиальной интерполяции для измерения показателей искусственной вентиляции легких // Биомедицинская радиоэлектроника. 2013, № И. С. 71 74.
- Лебединский К. М., Мазурок В. Л., Нефедов Л. В. Основы респираторной поддержки. — СПб.: Изд-во МАЛО, 2006. — 213 с.
- Mehta S.. Hill N. S. Noninvasive ventilation // Am J Respir Crit Care Med. 2001. Feb. 163(2). P. 540 577.
- Калиниченко Л. Н„ Немирно Л. П., Соломонова И. С. Использование полиномиальной интерполяции для измерения показателей искусственной вентиляции легких // Биомедицинская радиоэлектроника. 2013, № И. С. 71 74.
- Лебединский К. М., Мазурок В. Л., Нефедов Л. В. Основы респираторной поддержки. — СПб.: Изд-во МАЛО, 2006. — 213 с.
- Rapid Interpretation of Ventilator Waveforms / J. B. Waugh, V. M. Deshpande, M. K. Brown, R. J. Harwood. — N. J.: Upper Saddle River, 2007. — 151 p.
- Karason S., Sondergaard S., Lundin S., Slenqvist O. Continuous on-line measurements of respiratory system, lung and chest wall mechanics during mechanic ventilation // Intensive care medicine. 2001. V. 27. P. 1328-1339.
- Khirani S.. Polese G., Aiiverti A. et al. On-line monitoring of lung mechanics during spontaneous breathing: a physiological study // Respiratory medicine. 2010. V. 104. P. 463-471.
- Slenqvist O. Practical assessment of respiratory mechanics // British J. of Anaesth. 2003. V. 91 (I). P. 92-105.
- Манило Л. А., Немирно Л. П., Соломонова И. С. Автоматический анализ формы спирографических петель по их сигнатурам // Машинное обучение и анализ данных. 2013. Т. I, № 6. С. 687-694.
- Манило Л. Л., Немирно А. П., Соломонова И. С. Автоматический анализ формы спирографических петель при искусственной вентиляции легких // Изв. СПбГЭТУ «ЛЭТИ». 2013, № 8. С. 73-78.
- Лебединский К. М., Мазурок В. Л., Нефедов Л. В. Основы респираторной поддержки. — СПб.: Изд-во МАЛО, 2006. — 213 с.
- Rapid Interpretation of Ventilator Waveforms / J. B. Waugh, V. M. Deshpande, M. K. Brown, R. J. Harwood. — N. J.: Upper Saddle River, 2007. — 151 p.
- Гонсалес. Р., Вудс Р. Цифровая обработка изображений / Пер. с англ. — М.: Техносфера, 2005. — 1072 с.
- Rapid Interpretation of Ventilator Waveforms / J. B. Waugh, V. M. Deshpande, M. K. Brown, R. J. Harwood. — N. J.: Upper Saddle River, 2007. — 151 p.
- Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB / Пер. с англ. — М.: Техносфера, 2006. — 616 с.
- Rapid Interpretation of Ventilator Waveforms / J. B. Waugh, V. M. Deshpande, M. K. Brown, R. J. Harwood. — N. J.: Upper Saddle River, 2007. — 151 p.